Funktsiooni. Määratluspiirkond ja funktsioonide vahemik
Gbou Lyceum (majanduslik) lk. Isakla
Matemaatikaõpetaja Kuzaeva v.n.
2016 aasta
Võrdlusmaterjalid
ProovilahendusLeia palju funktsioone
Funktsiooniväärtuse ala 
on a
y. - mis tahes number
Funktsiooniväärtuse ala on a
y.
- mis tahes number
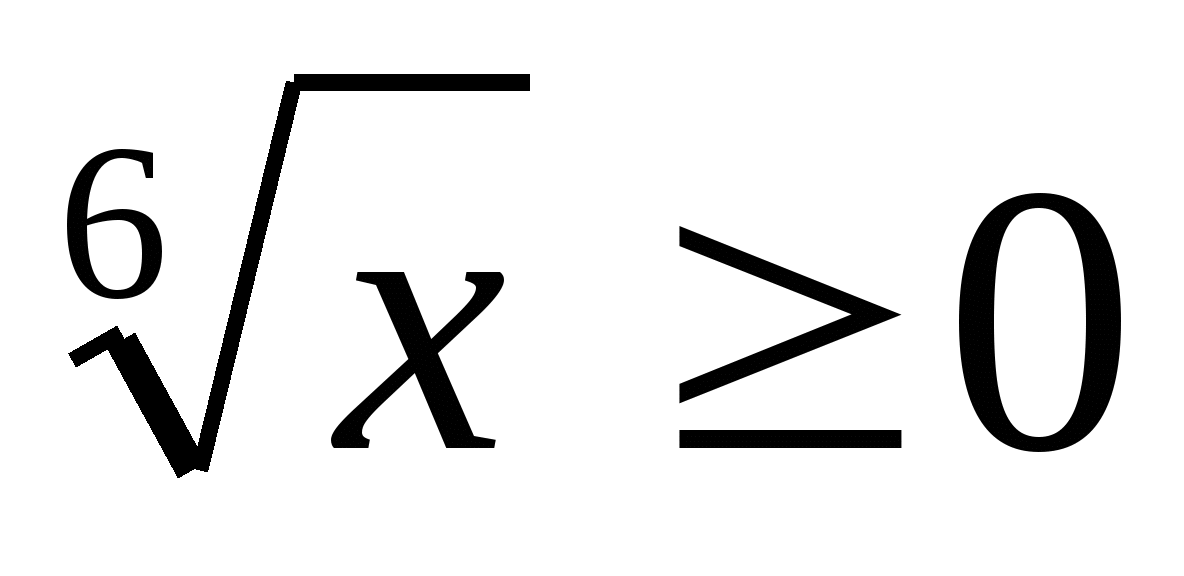
Paljud väärtused
y. - mis tahes number
Suurim väärtus
Väikseim väärtus
Domeen h.
- mis tahes number 
kus 
kus
Paljud väärtused 
y.
- mis tahes numbery.
- mis tahes number
Mõnede trigonomeetriliste funktsioonide graafikute mallid
Paljud trigonomeetriliste funktsioonide väärtused
valik 1
Y \u003dpatt.3x + 2.
1) (-5;5) 2) 3) 4) (1;5)
2. Asukoht funktsiooni väärtuse väärtus Y \u003dtG.x + 1.
1) 3) (-∞;∞) 4)
1) -6 2) 6 3) -4 4) -2
4. Määrake väikseim täisarv funktsiooniväärtuste funktsioonist.
y \u003d 12,7 + 5 patt.(3x-2).
1) -5 2) 8 3) 5 4) 17
5. Määrake funktsioon, mille kogum on segment [-2; 2].
1) y \u003d cos. 2x 2) y \u003d patt. 2 x. 3) y. = cos. 2 x. +2
4) y. = 2 patt. 4 x.
6. Leia funktsioonide kogumy. =
tG. 2
x. Lõigatud 
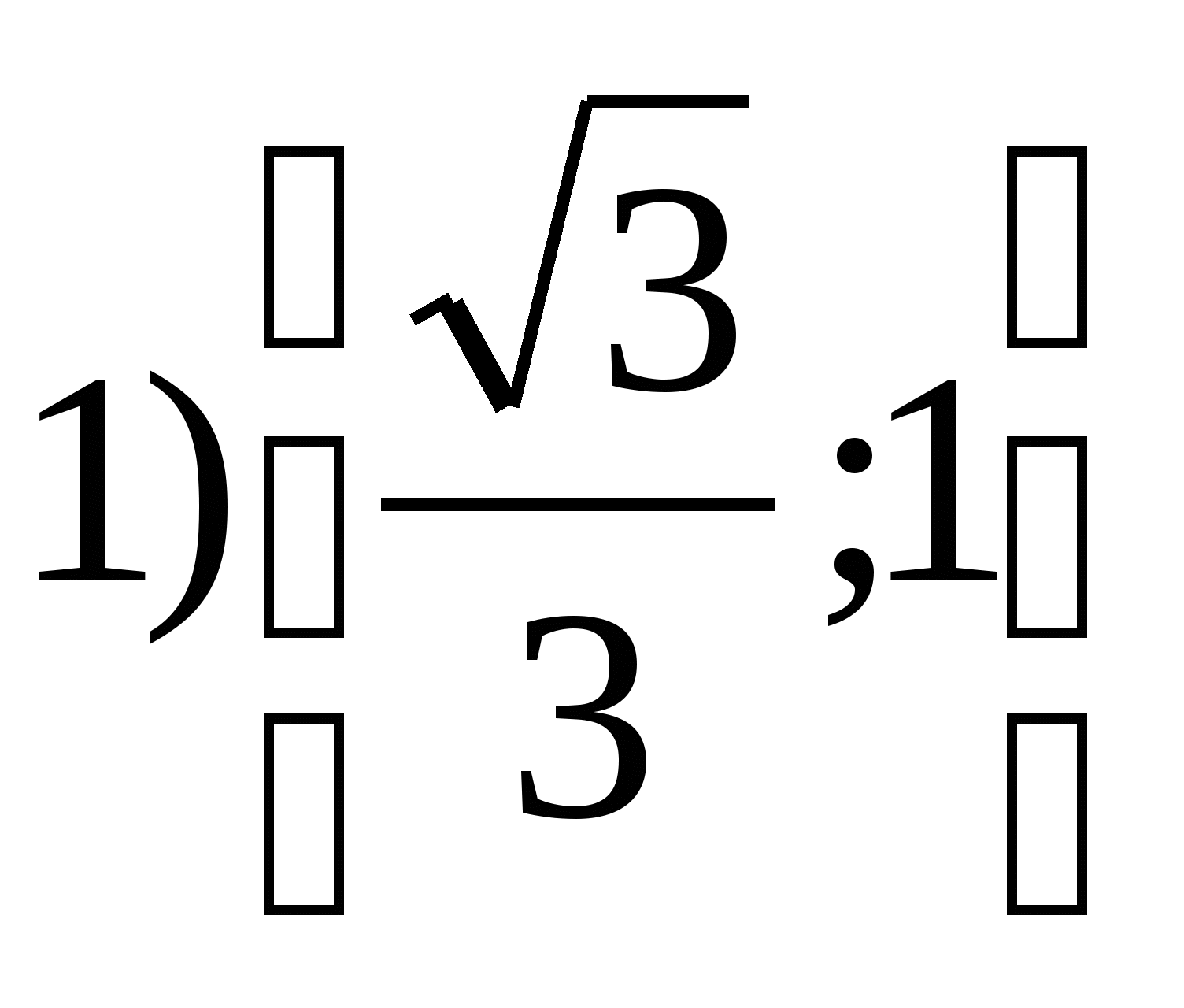
7. Leia kõigi funktsioonide väärtuste valdkonnas sisalduvate täisarvude summa.y. = 4 cos. 2 x. – 7.
1) -25 2) 25 3) -22 4) 0
2. võimalus.
y. = 2 cos. 5 x. +3.
1) (2;3) 2) 3) (1;5) 4) .
2. Leia ala väärtuse ala 
1) 3) (-∞;∞) 4) .
3. Määrake väikseim number funktsiooniväärtuste funktsioonist.
1) 4 2) -3 3) 1 4) -7
4. Määrake suurim täisarv funktsiooniväärtuste funktsioonist.
1) 2 2) 13 3) 12 4) -2
5. Määrake funktsioon, mille kogum on segment [-5; 5].
1) y \u003d sin 5x 2) y \u003d 5 cos 5x 3) y \u003d cos (-5x)
4) y \u003d sin 5x + 5
6. Leia funktsioonide kogum 
Lõigatud 
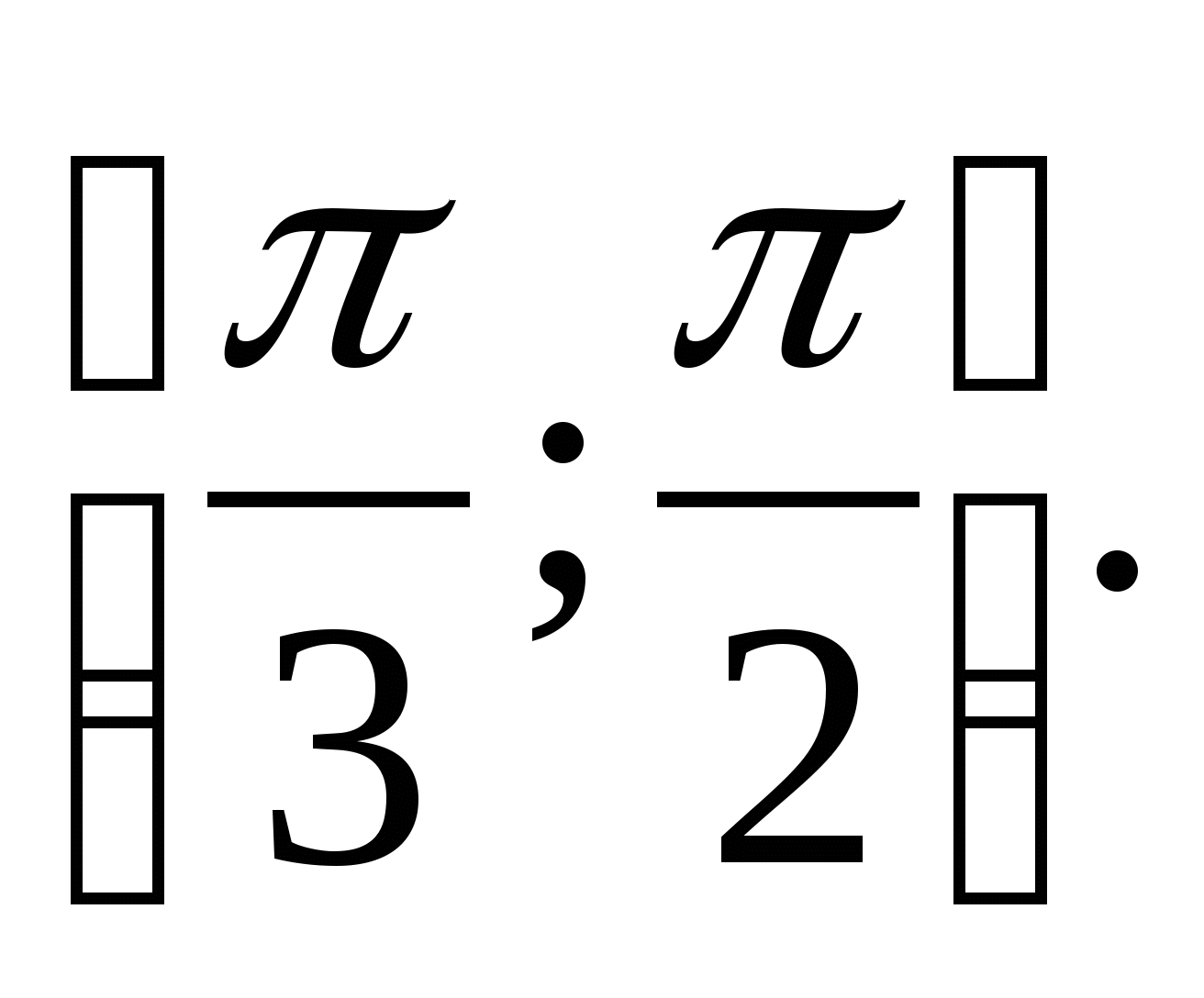
7. Leia kõigi täisarvude toote, mis kuuluvad funktsiooni funktsiooni Y \u003d 5 - 3patt. 2 x..
1) 120 2) 14 3) -15 4) 0
3. võimalus.
1. Määrake funktsioonide kogum.y. =
patt. 3
x. + 5.
1) (-4;6) 2) 3) [-1;5) 4) (0;6)
1) 2) (0;3) 3) (1;3) 4) [-1;3)
3. Määrake väikseim number funktsiooni funktsiooni funktsiooni Y \u003d 5tG. 2 x.+2?
1) 5 2) 0 3) 7 4) 2
1) -1 2) -2,7 3) -2,3 4)-3
5. Määrake funktsioon, mille kogum on segment
[-17;-13].
1) y \u003d 5 pattu x - 8 3) y \u003d -cos x +15
2) y \u003d 2 cos x - 15 4) y \u003d 3 pattu x +10
6. Määrake väikseim looduslik arv, mis ei kuulu funktsiooniväärtuste kogumile.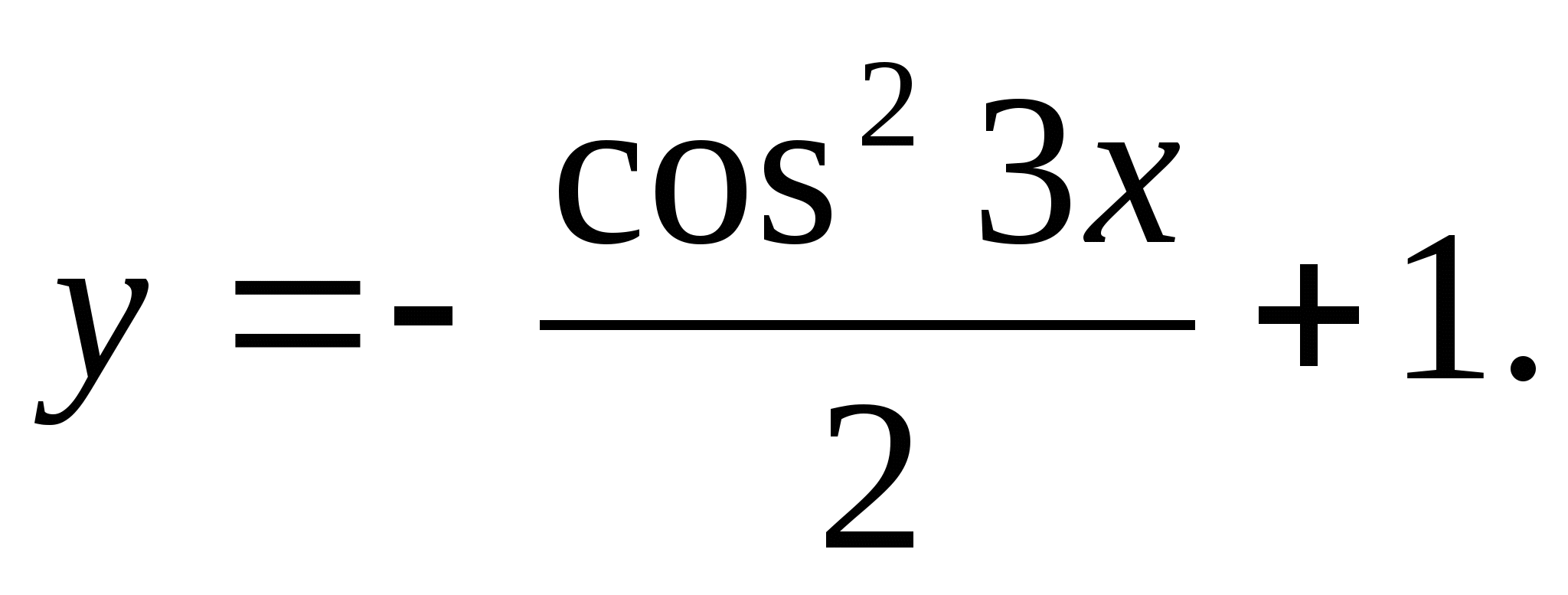 
1) 2 2) 4 3) 15 4) 6
7. Mitu täisarvu kuuluvad funktsiooniväärtuste kogumile
y. = 2 cos. 3 x. +10?
1) 2 2) 3 3) 4 5) 5
Võimalus 4.
1) 2) 4) (-7;-6)
2. Leia erinevaid funktsiooni väärtusi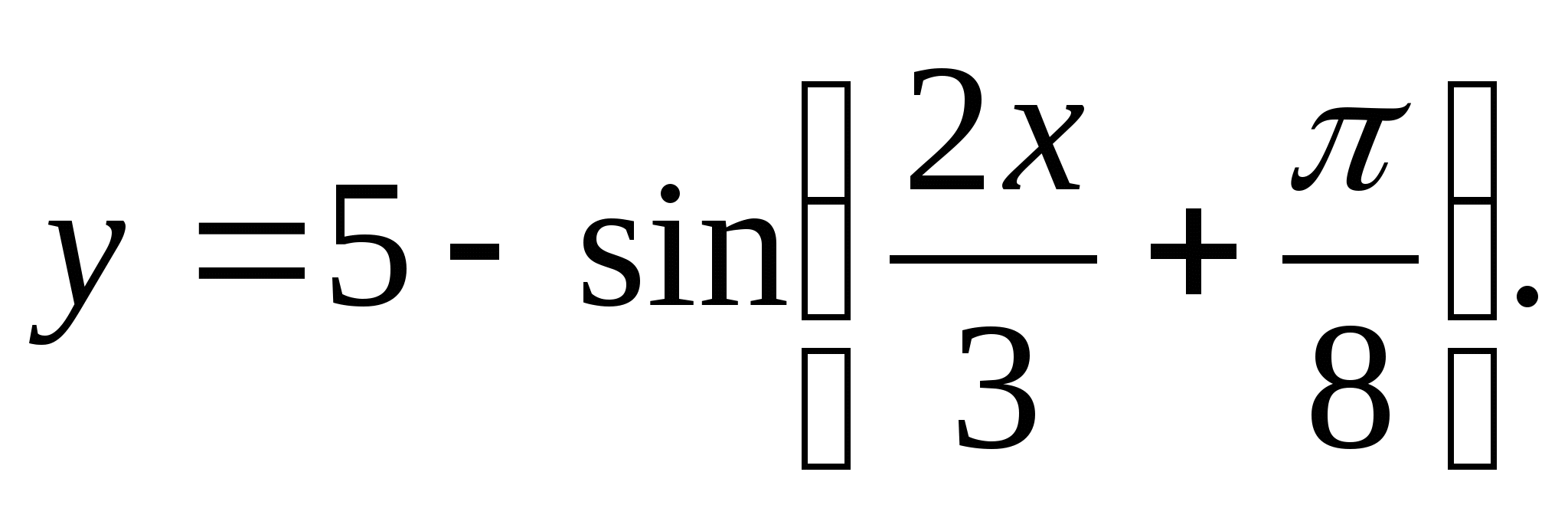 
1) (1;5) 2) 3) (4;6) 4) [-6;-4]
3. Määrake suurim number funktsiooniväärtuste funktsioonist.y. = -3 cTG. 2 x.+7.
1) 10 2) 4 3) 7 4) -3
4. Milline järgmistest numbritest ei kuulu funktsiooniväärtuste komplekt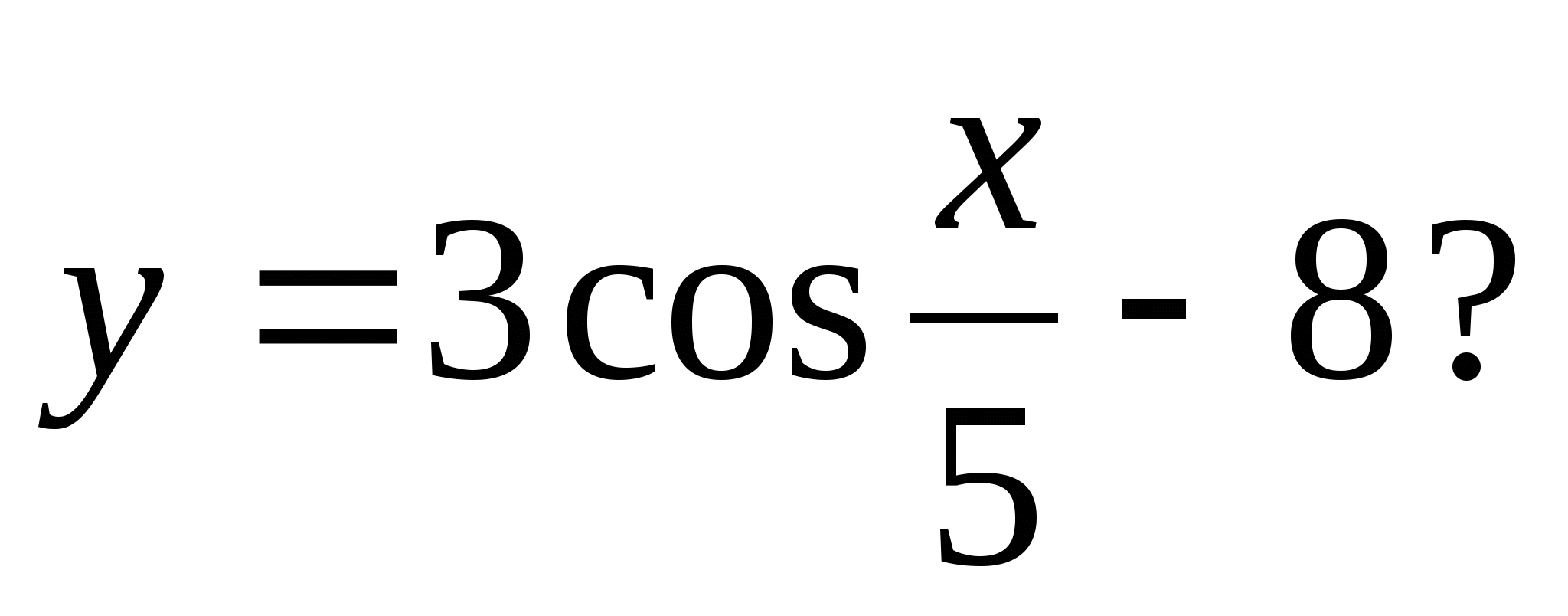 
1) -6 2) -5 3) -10 4) -7
5. Määrake funktsioon, mille kogum on segment.
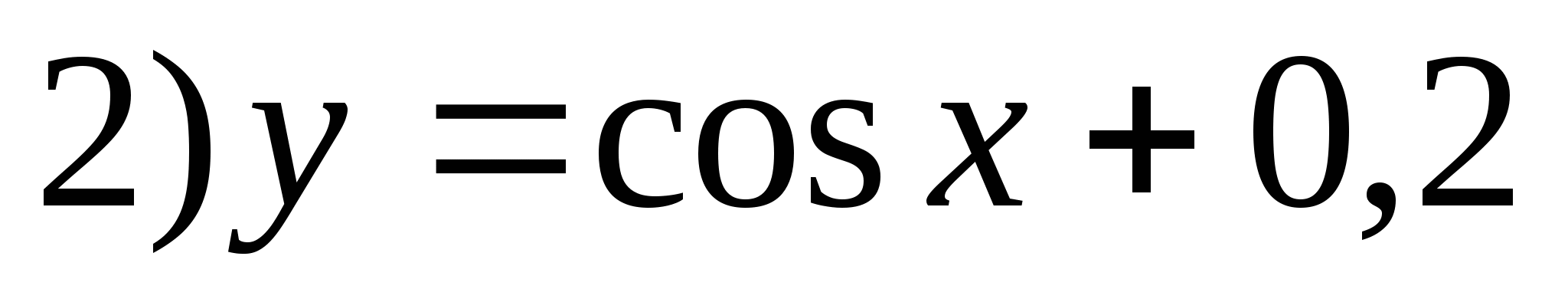
6. Määrake suurim täisarvu negatiivne number, mis ei kuulu funktsiooniväärtuste valdkonnas. 
1) -1 2) -25 3) -6 4) -2
7. Mitu täisarvu kuuluvad funktsiooniväärtuste kogumile 
1) 11 2) 3 3) 5 4) 4
Võimalus 5.
1. Täpsustage funktsiooni väärtuste kogum Y \u003d 2 -patt. 5 x..
1) (2;5) 2) 3) (1;3) 4) [-3;7]
2. Leia erinevaid funktsiooni väärtusi 
1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)
3. Määrake väikseim täisarv funktsiooniväärtuste funktsioonist.
y. = 3 + patt. 2 2 x..
1) 0 2) 1 3) 3 4) 4
4. Milline järgmistest numbritest siseneb funktsiooni palju väärtusi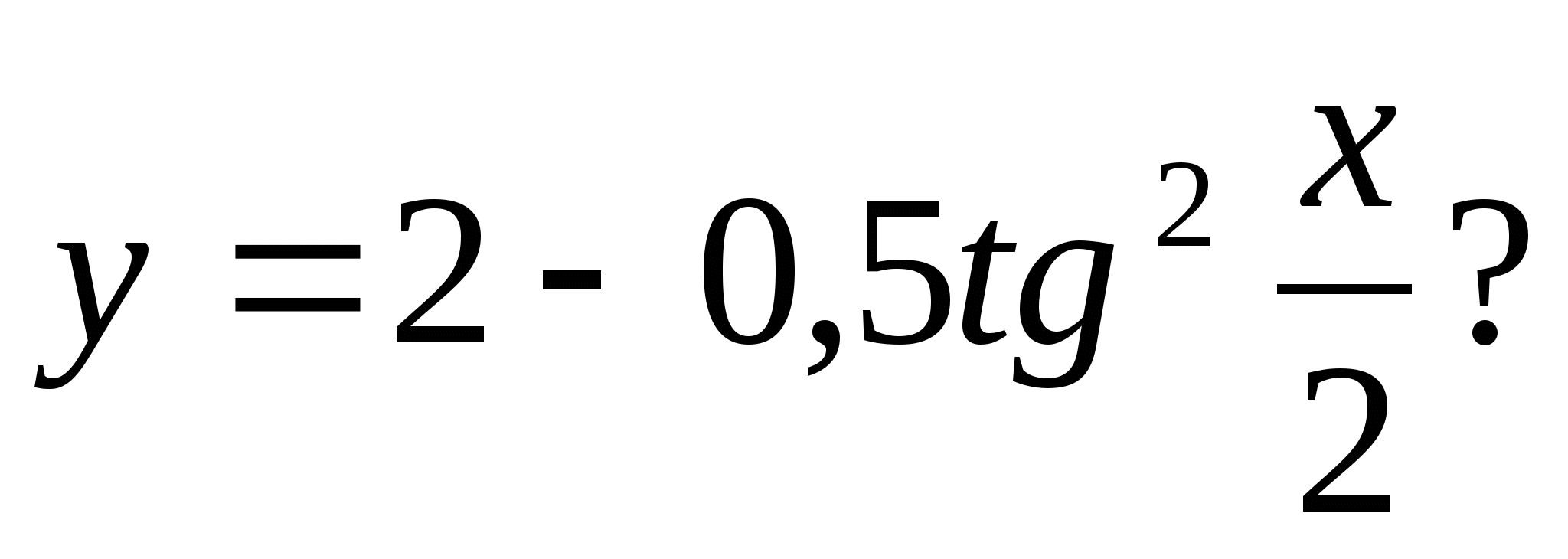 
1) 128 2) 10,5 3) 3 4) -235
5. Määrake funktsioon, mille kogum on segment [-9; 15].
6. Leidke funktsiooniväärtuste komplektis sisalduvate täisarvude kogus 
1) 0 2) 7 3) 18 4) 22
7. Leia funktsiooni suurim väärtus. 
lõigatud 
1) 0,5 2) 1,5 3) 0 4) 2
6. võimalus.
1. Määrake segment, mis vastab funktsiooniväärtuste kogumile 
1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]
2. Leia erinevaid funktsiooni väärtusi 
3. Määrake suurim number funktsiooniväärtuste funktsioonist.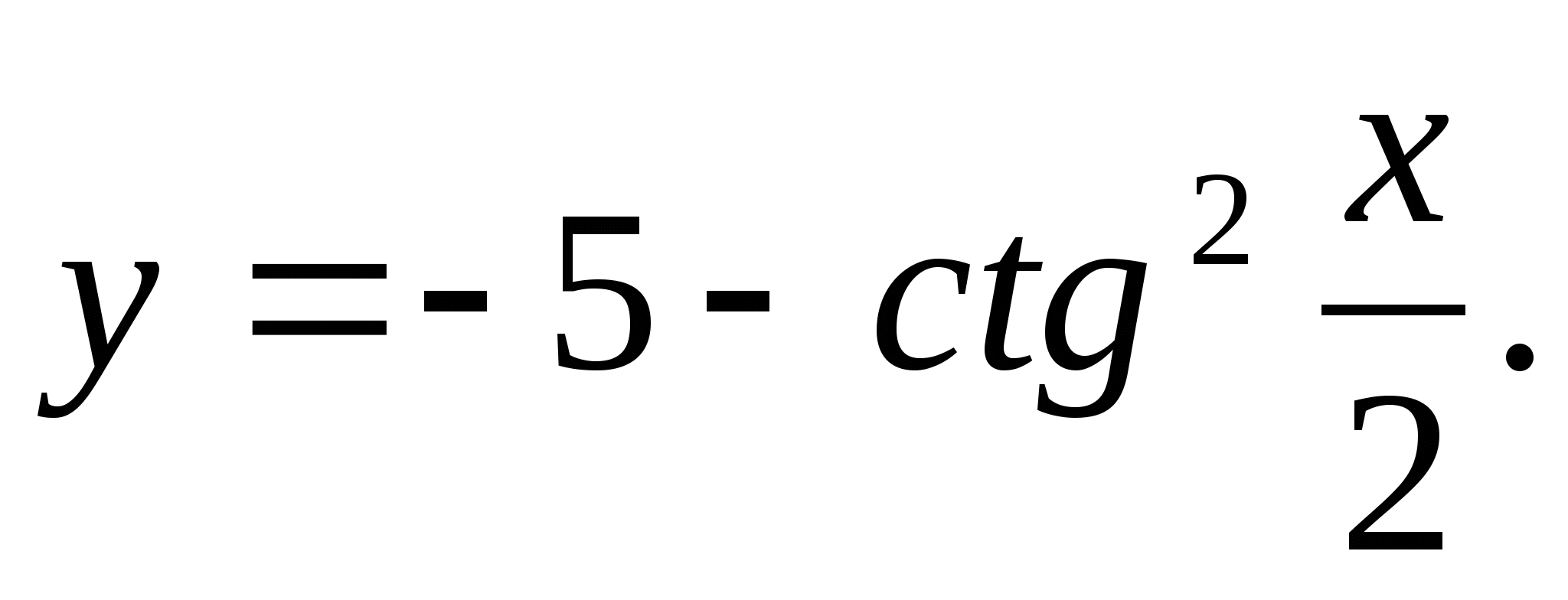 
1) 5 2) -6 3) -3 4) 4
4. Milline järgmistest numbritest siseneb funktsiooni palju väärtusi 
1) 5 2) 0 3) -3 4) 4
5. Määrake funktsioon, mille kogum on segment.
1) w. \u003d 15 - 7 cos 2x 3) y \u003d 7 cos 2x + 3
2) y. = 5 cos. 4 x. 4) y. = - tG. 2 x. + 1
6. Leia paljude väärtuste kaasatud täisarvude toode.
y. = 3,8 – 1,4 patt. 3 x..
1) 17 2) 12 3) 0 4) 60
7. Leia funktsioonide kogum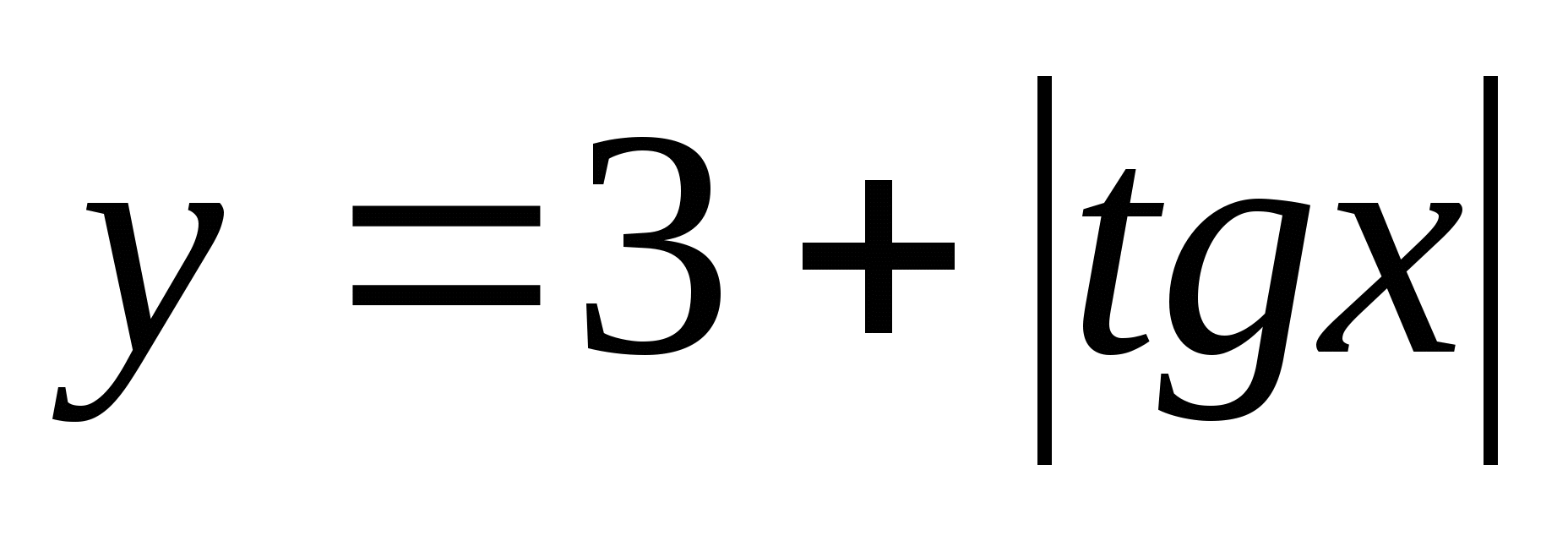 
Intervallil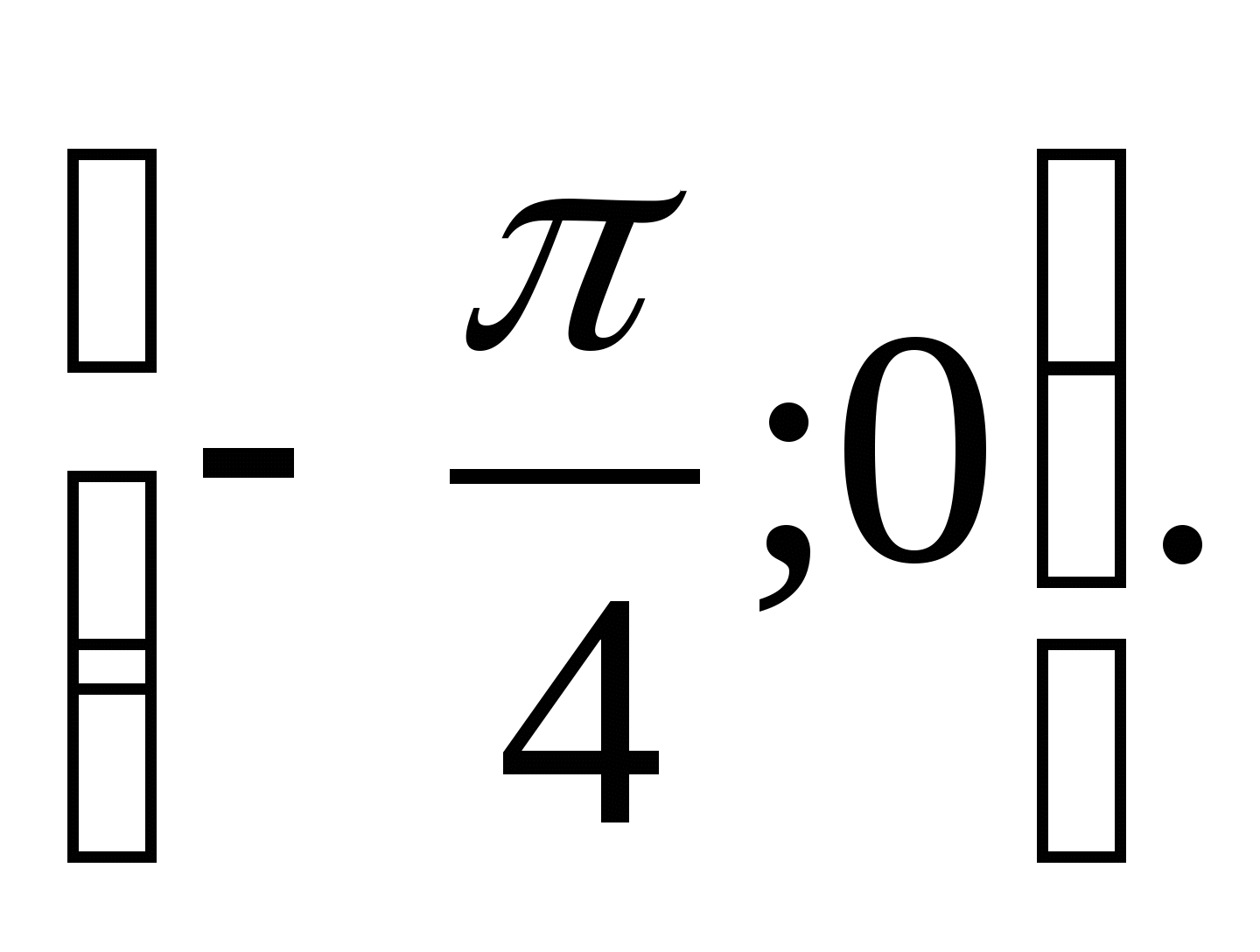 
1) (3;4) 2) 3)
Võimalus 7.
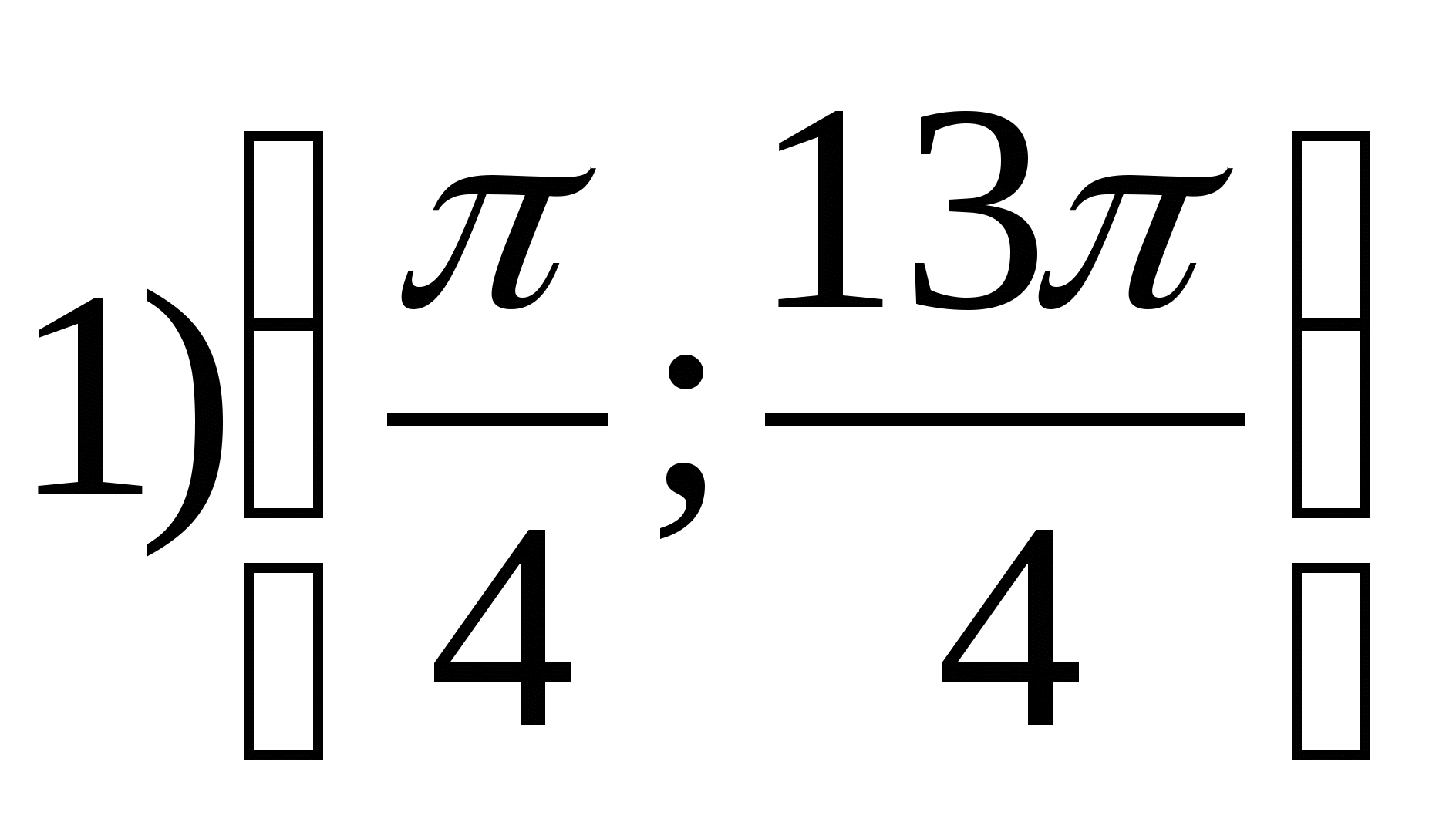
2. Leidke funktsiooni väikseim väärtus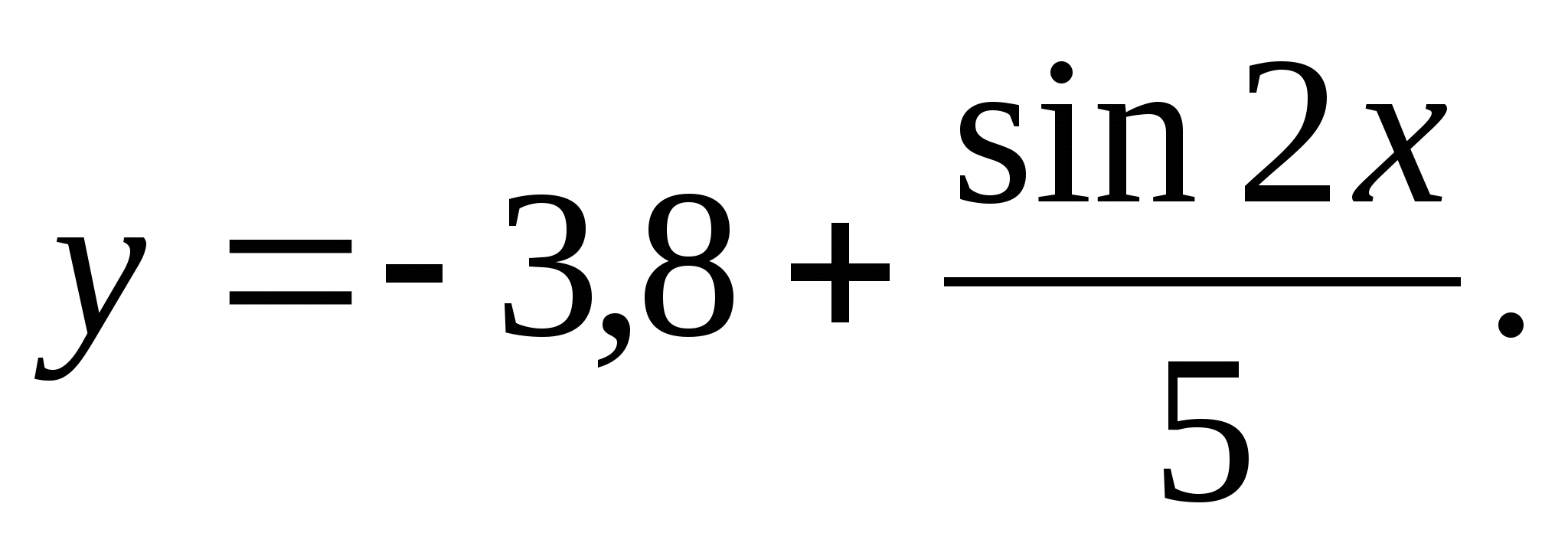 
1) 2 2) 0 3) -3 4) -4
1) 0 2) 2 3) 4 4) 6
4. Millistel väärtustel ja võrrandispatt.(3 x.-4)+5= a. lahendatav?
1) 2) 3) (4;6) 4) (-6;4]
patt. 2 2 x. – 2.
1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]
Intervallil 
2) 0 3) 1
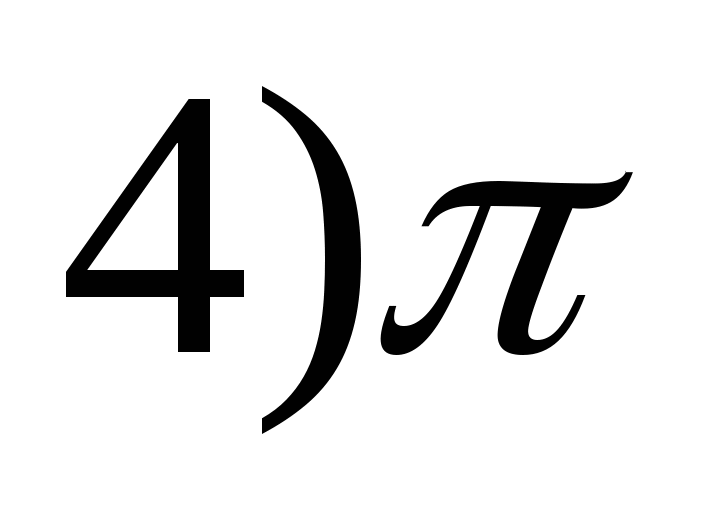
y. = 4 patt.(x. 4 ) -2?
1) 8 2) 9 3) 7 4) 10
Võimalus 8.
1. Leia funktsioonide kogumy. = aRCTG.x. - 2π.
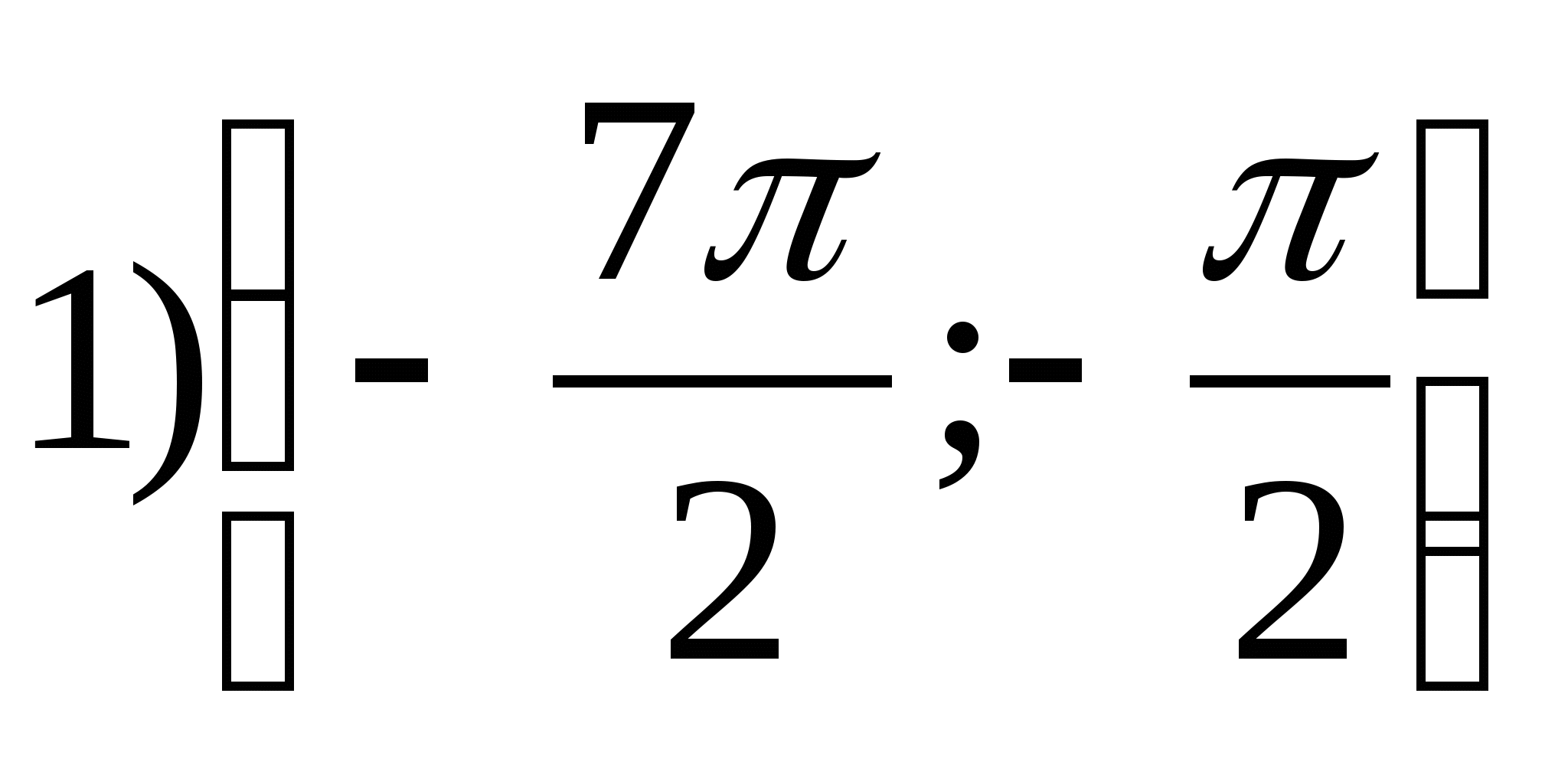
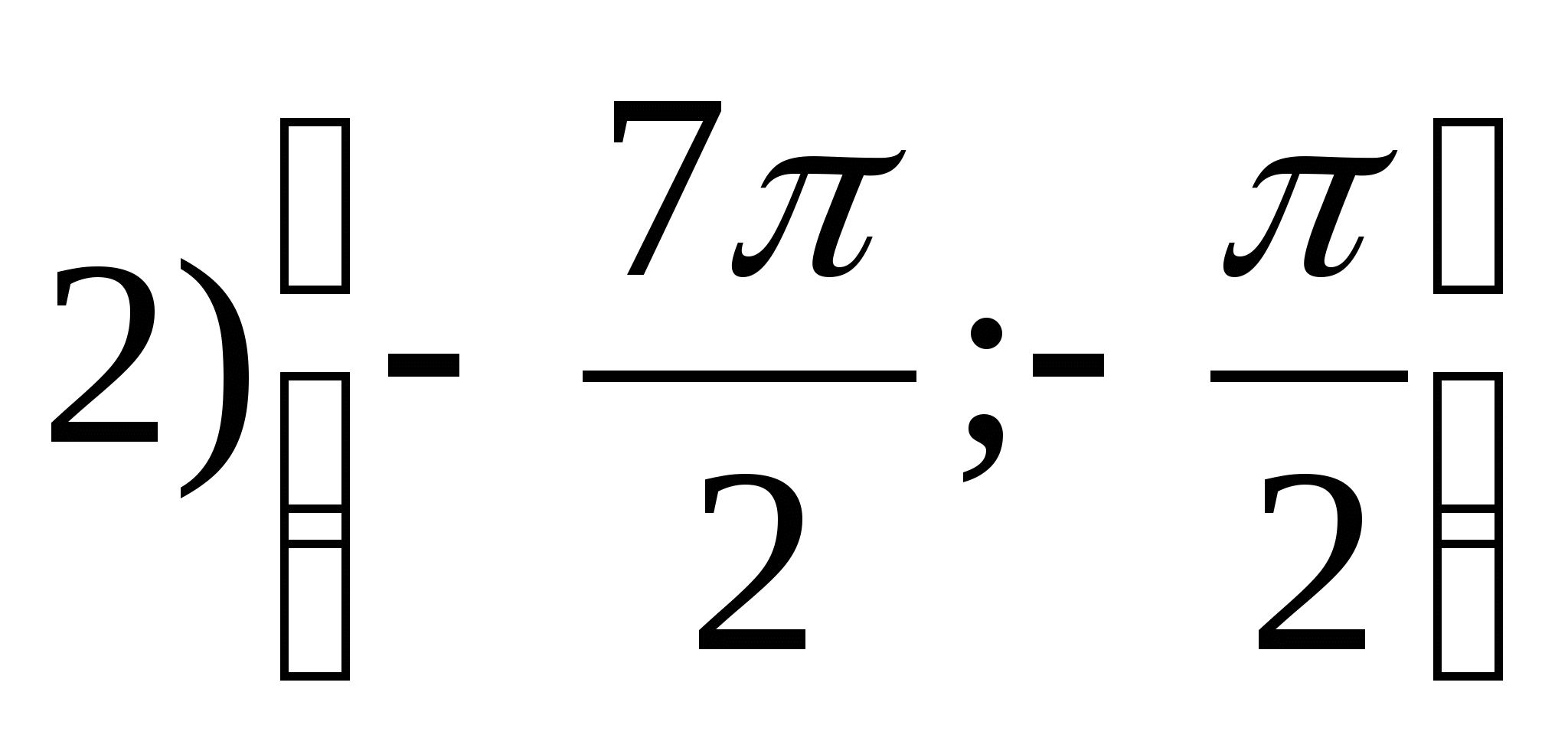
2. Leidke funktsiooni suurim väärtus.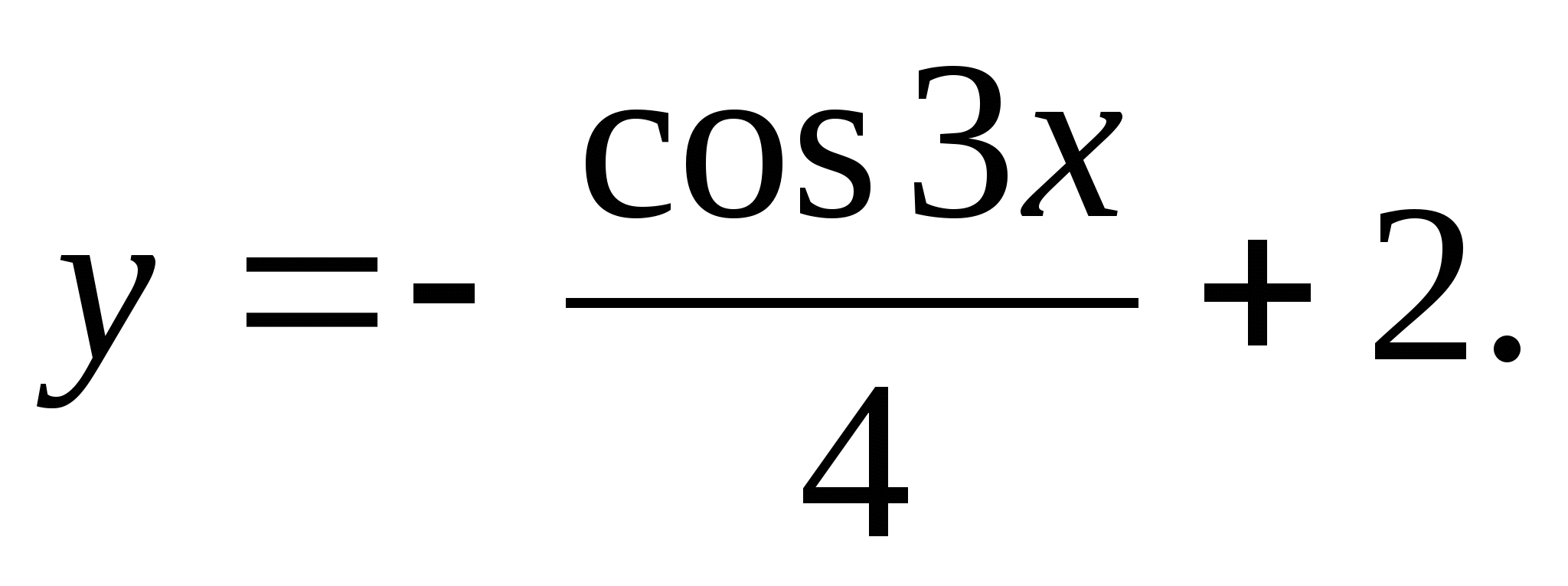 
1) 1,75 2) 0 3) 2,25 4) -1,75
3. Milline järgmistest numbritest võib olla funktsiooni väärtus 
1) -4 2) -2 3) 0 4) 2
4. millistel väärtustel p võrrandi -2+cos.(4 x.-1)= p. Kas juured on?
1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)
5. Leidke erinevaid funktsiooni väärtusi.y. = -2 tG. 2 x. + 1.
1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)
Intervallil 
.
1) 0 2) 1 3) -1 4) 3
7. Mitu täisarvu kuulub funktsioonide valdkonda
1) 4 2) 3 3) 5 4) 2
1. võimalus.
1. Leia funktsiooni väärtuste funktsioon. 
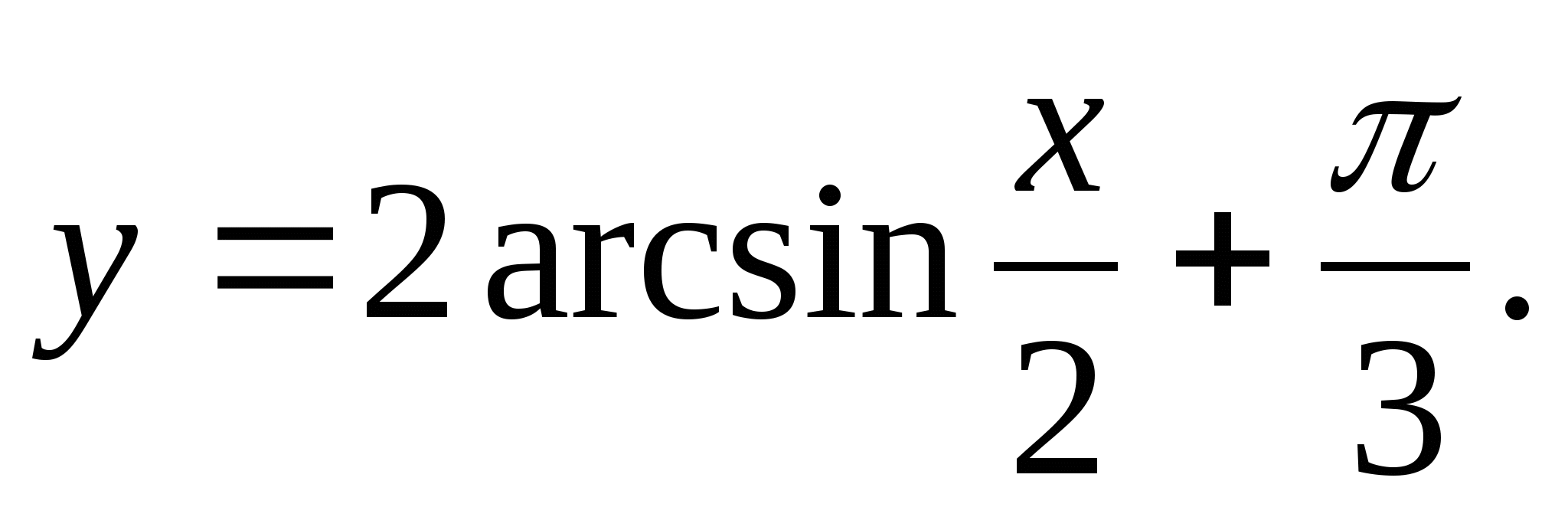
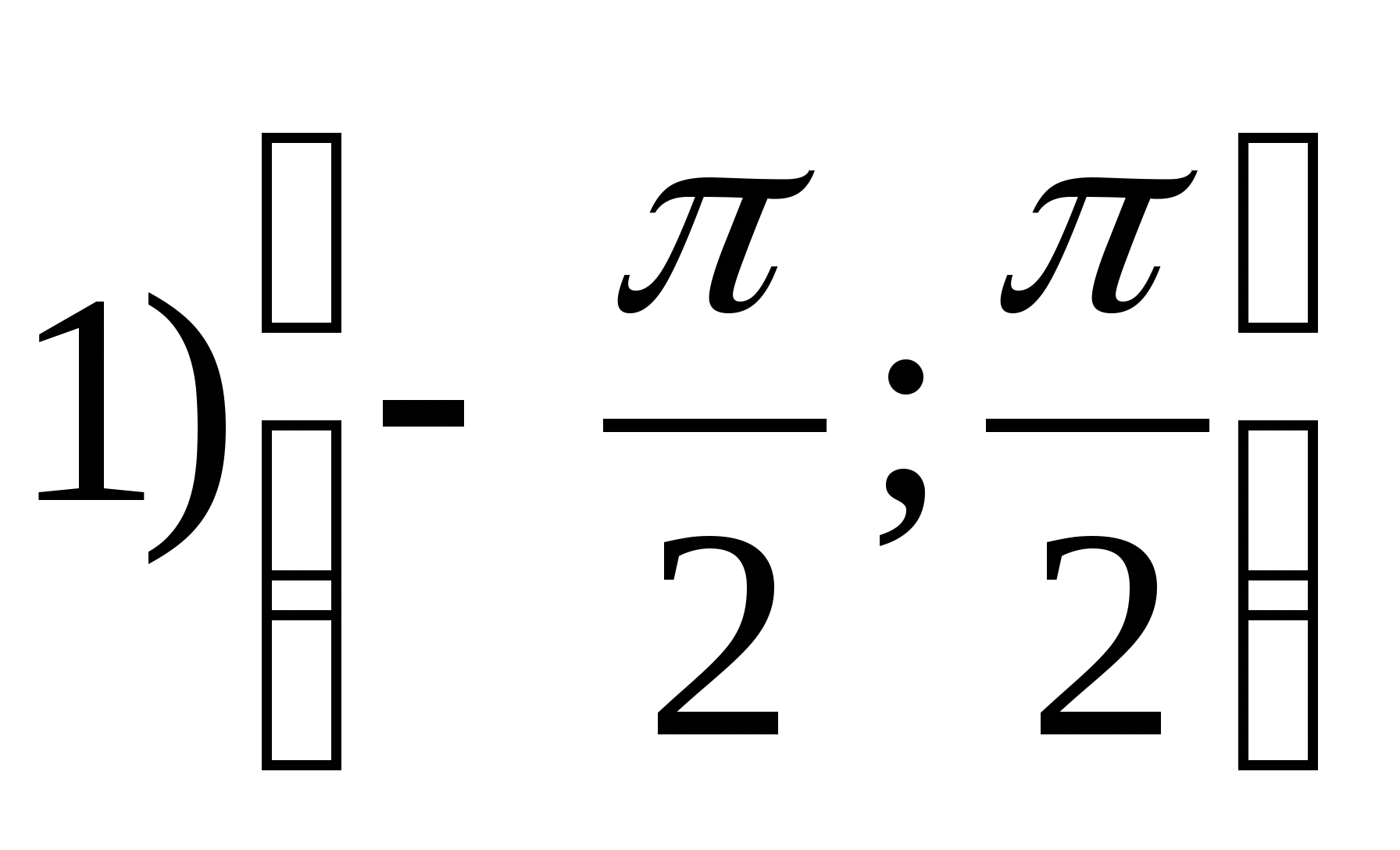
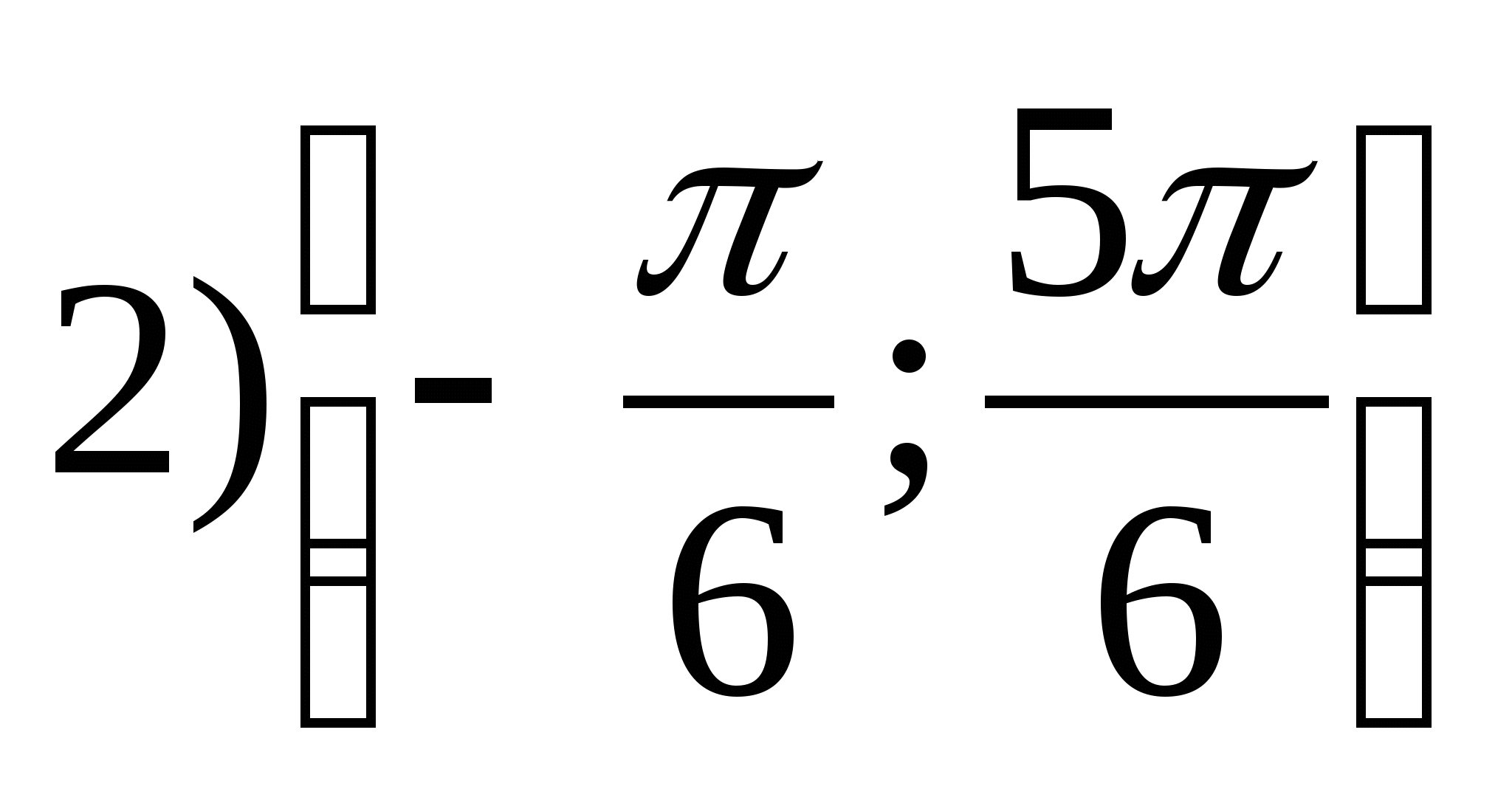
2. Leidke funktsiooni suurim väärtus 
1) 4 2) 5 3) 6 4) 7
3. Milline järgmistest numbritest võib olla funktsiooni väärtus 
1) 0 2) 3 3) 6 4) 9
k. Võrrand - k. + patt.(2 x.-1) \u003d 2 lahendatav?
1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]
5. Leia paljude funktsioonide väärtused Y \u003d -cos. 2 3 x. + 4.
1) 2) 3) 4)
6. Määrake funktsiooni väikseim väärtus. intervallil 
2) -1 3) 0 4) 1
7. Leia, kui palju täisarvude lisatakse funktsiooni funktsiooni funktsiooni Y \u003d 12cos. 3 x. +5 patt. 3 x..
1) 13 2) 27 3) 26 4) 14
Võimalus 10.
1. Leia funktsiooni väärtuste funktsioon. 
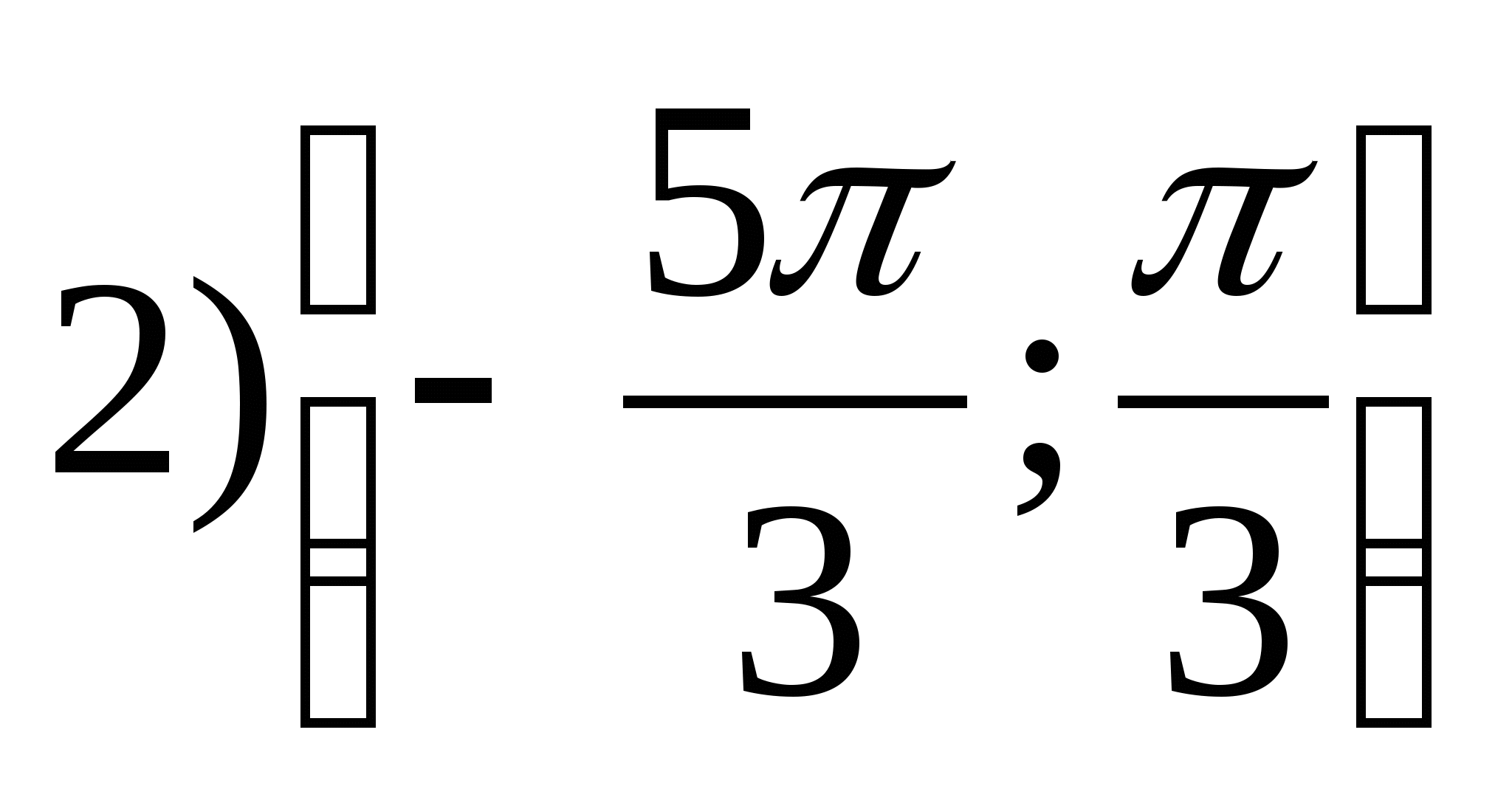
2. Leia väikseim funktsiooni väärtus 
1) 3,5 2) 0 3) 2,5 4) -3,5
3. Milline järgmistest numbritest võib olla funktsiooni väärtus 
1) -4 2) -1 3) 3 4) 7
4. Millistel parameetri väärtustelm. võrrand cos. (3 x. + 2)- m. \u003d 5 on juured?
1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]
5. Leidke funktsiooni Y \u003d -2cTG. 2 3 x. + 7.
1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]
6. Määrake funktsiooni suurim väärtus. 
Intervallil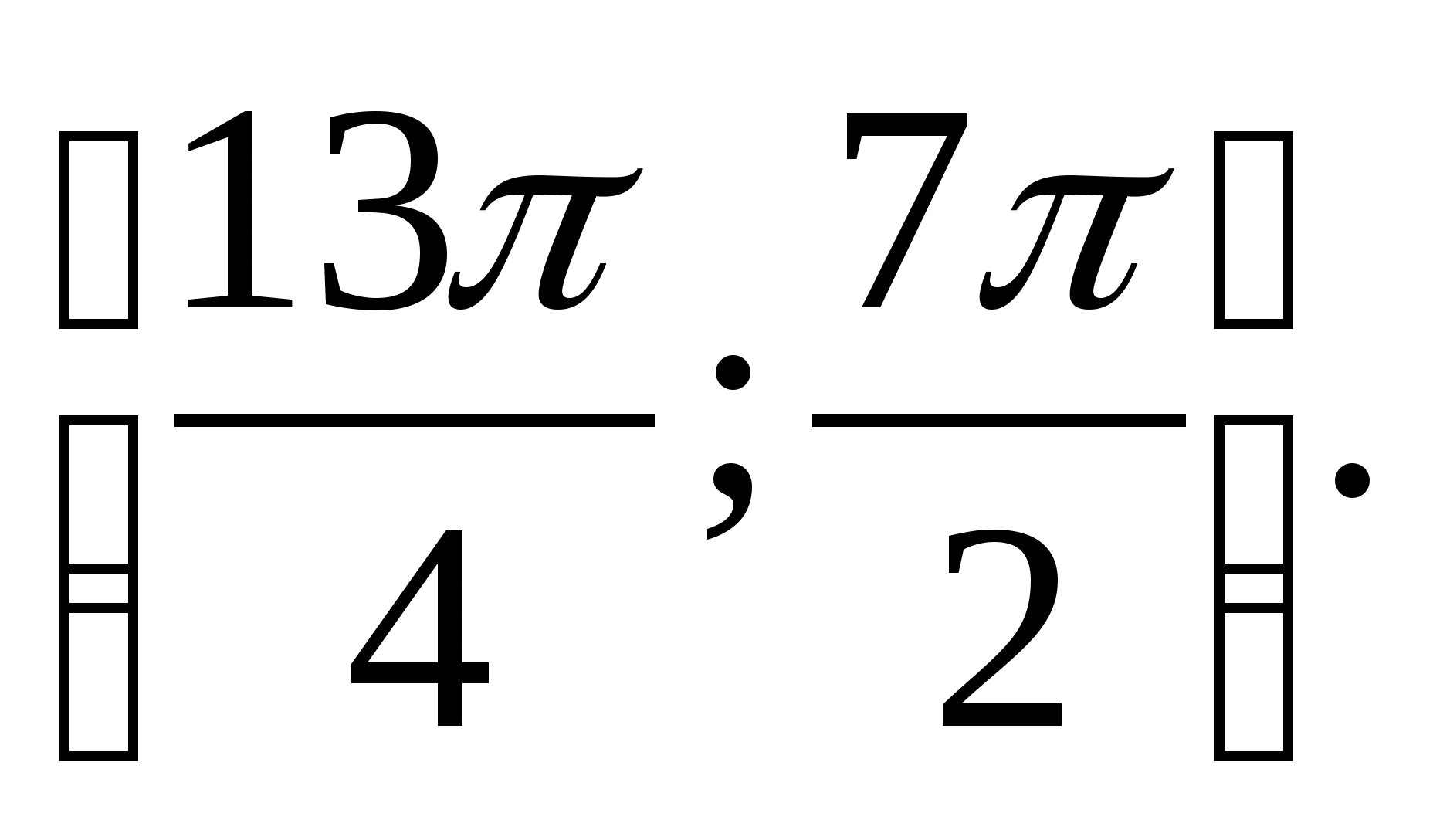 
2) 0 3) 2 4) 1
7. Leia, kuidas paljud täisarvud on funktsiooni väärtuste valdkonnas kaasatud. 
1) 30 2) 35 3) 17 4) 7
Paljud soovituslike ja logaritmiliste funktsioonide väärtused
valik 1
1. Leia funktsiooni väärtuste funktsioon. 
1) 4) (-∞;3)
2. Määrake funktsioonide kogum.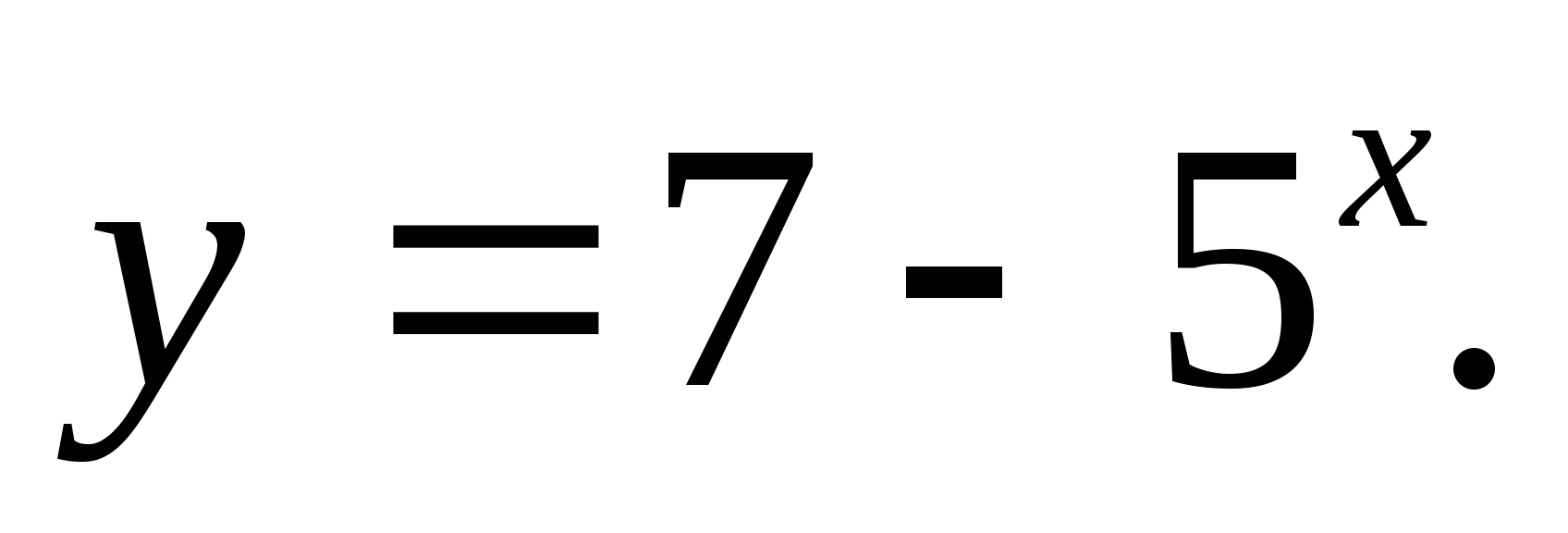 
1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]
1) 0 2) 4 3) -3 4) -4
1) 15 2) 20 3) 43 4) 28
1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)
6. Määrake funktsiooni väikseim väärtus 
1) 1 2) -1 3) 0 4) -5
7. Täpsustage funktsioon, mille väärtused on intervalli (1; ∞).
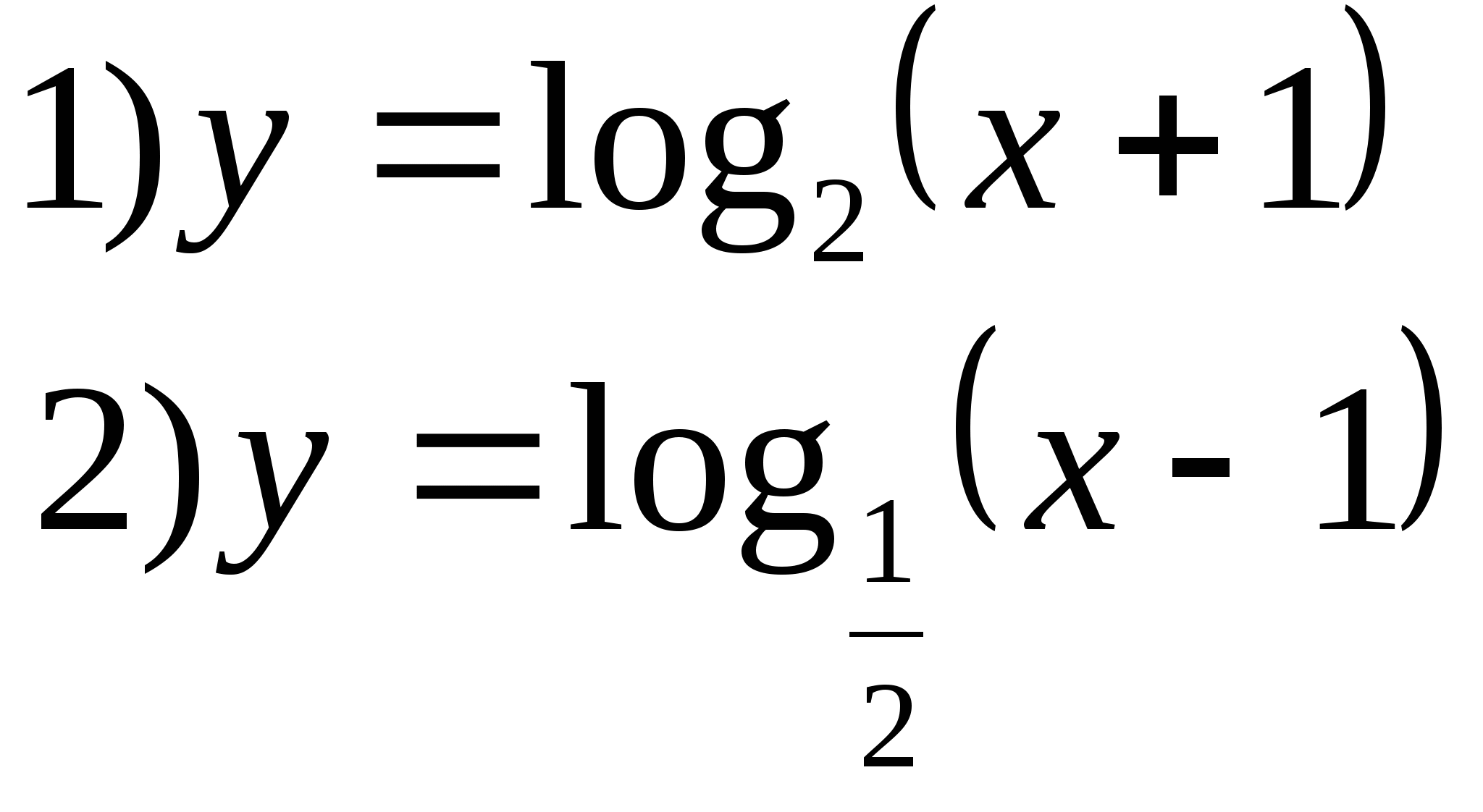
2. võimalus.
1. Määrake funktsioonide kogum. 
1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)
2. Leia erinevaid funktsiooni väärtusi 
1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)
3. Määrake funktsiooni väikseim väärtus 
1) -12 2) -11 3) -10 4) -15
4. Määrake number, mis ei kuulu funktsionääride komplekt 
1) -42 2) 3 3) 1 4) -20
5. Määrake funktsioonide kogum. 
1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]
6. Määrake funktsiooni suurim väärtus. 
1) 10 2) 3 3) 9 4) 2
7. Määrake funktsioon, mille kogum on lõhe.
(-∞;13).
Võimalus 5.
1. Määrake funktsiooni väikseim väärtus 
1) 0 2) -1 3) -2 4) -3
2. Milline järgmistest numbritest siseneb funktsiooniväärtuste valdkonnas 
1) -3 2) -4 3) 5 4) 0
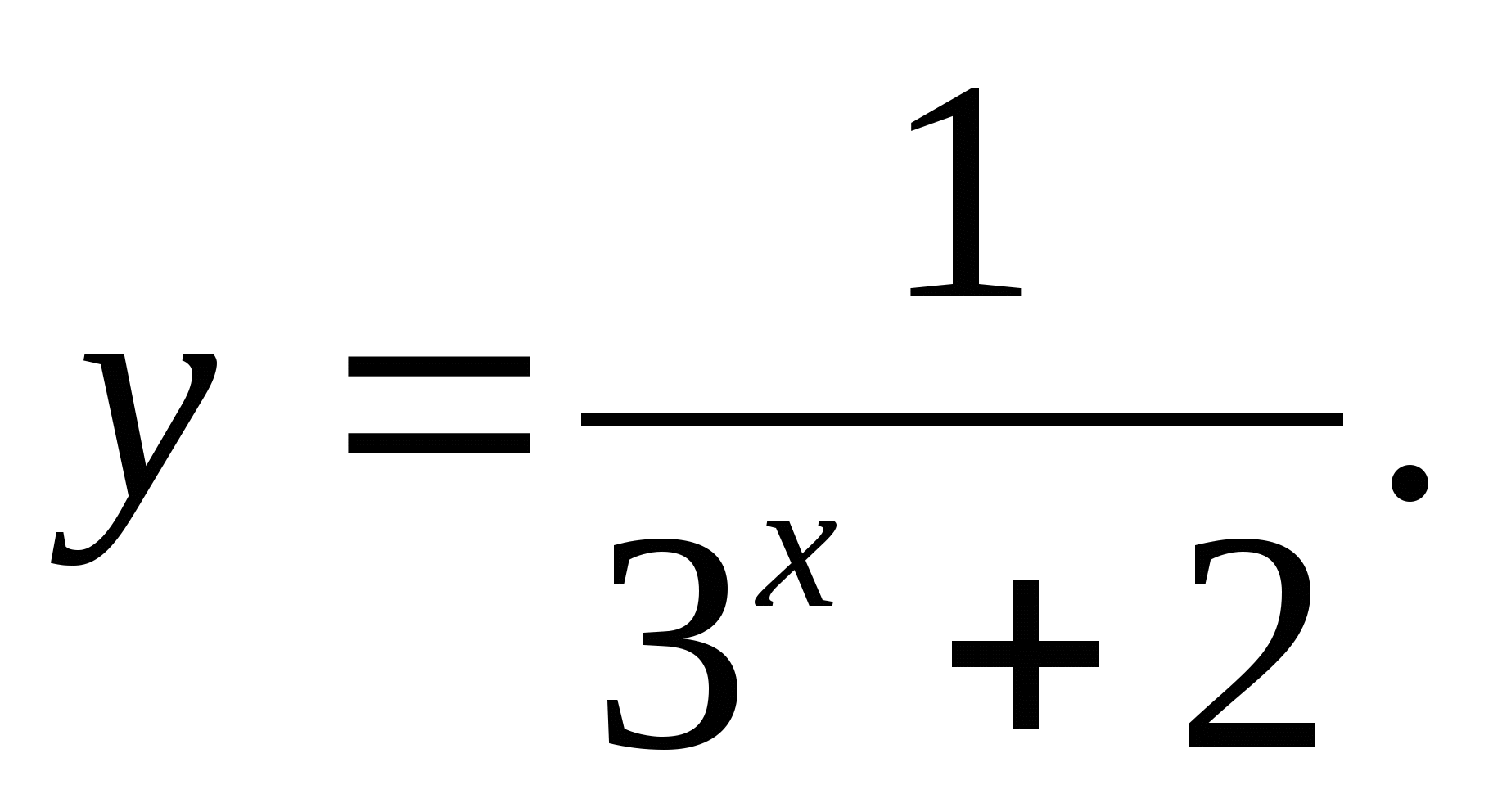
1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)
6. Leia, mis sektsioon on funktsioon 
See võtab suurim väärtus võrdne 2-ga ja väikseim väärtus võrdub -3-ga.
1) 2) (-5;2) 3) 4) (-3;2)
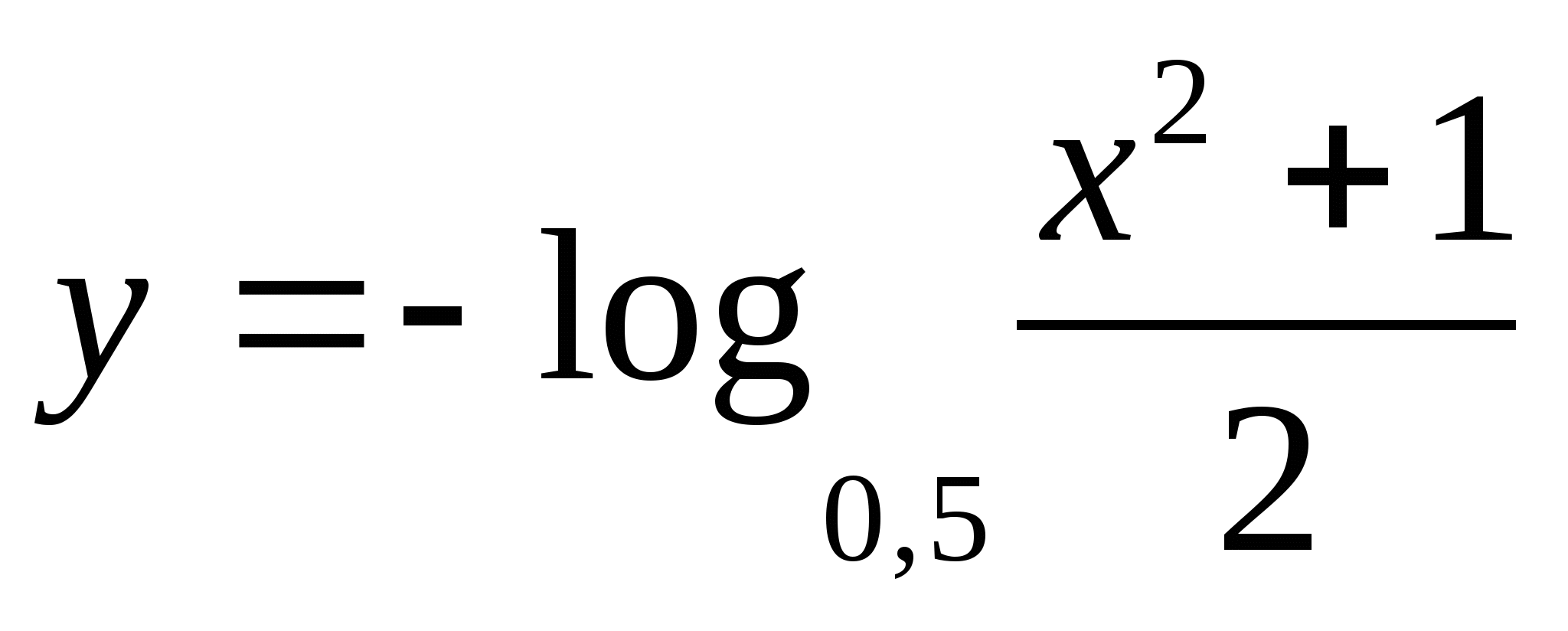intervallil 
1) -1/2 2) 5 3) 2 4) 4
8. Leidke kõigi looduslike numbrite summa, mis ei kuulu funktsiooniväärtuste komplekti. 
1) 3 2) 6 3) 10 4) 8
6. võimalus.
1. Määrake funktsiooni suurim väärtus. 
1) 2 2) 4 3) 3 4) 5
2. Milline järgmistest numbritest ei kuulu funktsioonide väärtuste vahemikus 
1) 35 2) 7, 28 3) 7, 85 4) 128
3. Määrake funktsioonide kogum. 
1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)
4. Leia kõik OS-i punktid, mis on taasesituspunktide prognoosid 
1) (0;∞) 2) 2) (-3;2) 3) [ logige sisse. 2 3;2] 4) (logige sisse. 2 3;2)
6. Leidke funktsioon, millises segmendis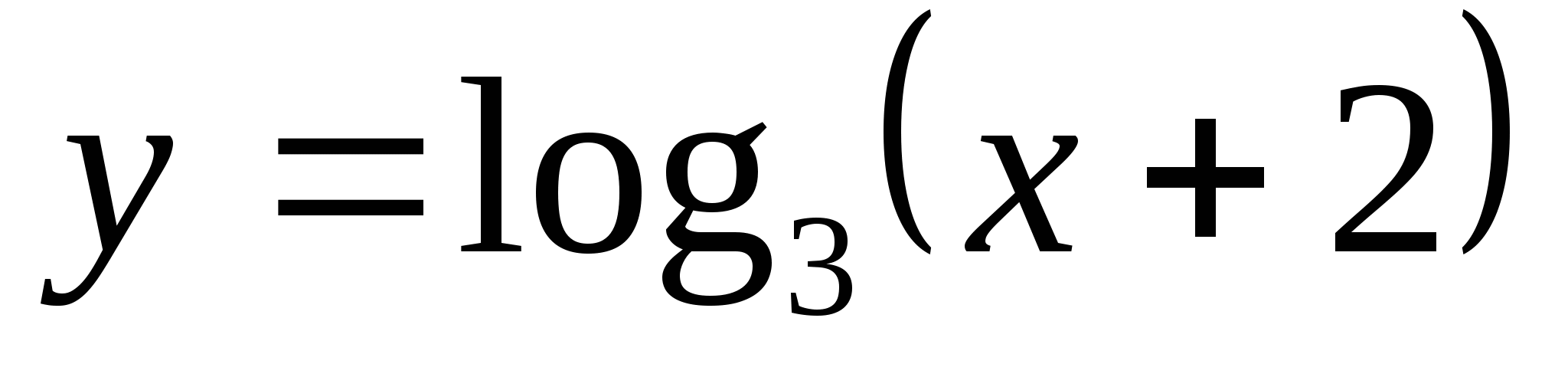 
see võtab väikseima väärtuse võrdne -2-2 ja suurim väärtus võrdne 4-ga.
1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)
7. Määrake funktsiooni suurim väärtus. 
Intervallil
[-0,9; 0]. 2. Leidke segmendi väikseim funktsiooni väärtus.
4. Kui palju väärtusi funktsiooni võtab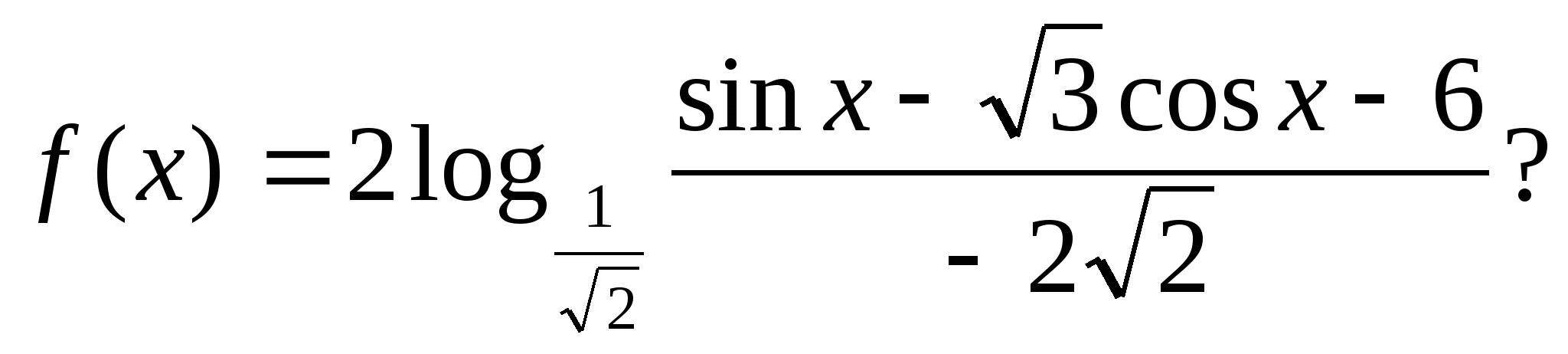 
Vastused
1. osa
Paljud soovitusliku ja logaritmilise funktsiooni väärtused
2. osa
Ülesanne Y \u003d F (x) on muutuja Y-i muutujast sõltuvus X-st, kui iga varieeruva X lubatud väärtus vastab muutuva muutuja ainsele väärtusele.
Funktsioonide määratluspiirkond D (f) Helista kõigi muutuja X kehtivate väärtuste kogum.
Funktsiooniväärtused E f) - muutuva varieeruva lubatud väärtuste kogum.
Ajakava funktsioon Y \u003d f (x) - paljude tasapindade punkte, mille koordinaadid vastavad sellele funktsionaalsele sõltuvusele, st punktid, vormi M (x; f (x)). Funktsioonide graafik on tasapinnal mõnda rida.
Kui b \u003d 0, siis funktsioon võtab vormi Y \u003d KX ja nimetatakse otsene proportsionaalsus.
D (f): x \\ in r; Enspace e f): y \\ in r
Lineaarse funktsiooni graafik on sirge.
Nurk koefitsient K Otse Y \u003d KX + B arvutatakse järgmise valemi abil:
k \u003d tg \\ alfa, kus Alpha on kaldenurk otsene positiivse suuna Ox-telje.
1) funktsiooni monotoonselt suureneb k\u003e 0 juures.
Näiteks: Y \u003d X + 1
2) funktsiooni monotoonselt väheneb, kui< 0 .
Näiteks: Y \u003d -X + 1
3) Kui k \u003d 0, siis andes b meelevaldseid väärtusi, saame otsese paralleelse telgi oksi perekonna.
Näiteks: Y \u003d -1
Pöörde proportsionaalsus
Pöörde proportsionaalsus nimetatakse tüübi tüübile y \u003d frac (k) (x)kus K erineb nullist, kehtiv number
D f): x vasakule \\ (r / x \\ rEQ 0 \\ õige); \\: E (f): y \\ vasanud \\ (R / Y \\ NEQ 0 \\ õige).
Graafik y \u003d frac (k) (x) on hüperbool.
1) Kui k\u003e 0, asub funktsiooni ajakava koordinaatitasandi esimeses ja kolmandas kvartalis.
Näiteks: y \u003d Frac (1) (x)
2) kui k< 0 , то график функции будет располагаться во второй и четвертой координатной плоскости.
Näiteks: y \u003d - \\ Frac (1) (x)
Võimsusfunktsioon
Võimsusfunktsioon - See on vormi Y \u003d x ^ n funktsioon, kus n on erinev nullist, kehtiv number
1) Kui n \u003d 2, siis y \u003d x ^ 2. D (f): x r; \\: E f): y \\ in; Funktsiooni peamine periood t \u003d 2 pi
Sageli peame probleemide lahendamise osana otsima mitmeid määratluse või segmendi funktsiooni väärtusi. Näiteks tuleb seda teha erinevate ebavõrdsuse lahendamisel, väljendite hindamiseks jne.
Selle materjali osana kirjeldame, et funktsiooni väärtuste valdkond kujutab endast põhilisi meetodeid, mida saab arvutada, ja me analüüsime erineva keerukuse kraadi ülesandeid. Selguse huvides on individuaalsed positsioonid illustreeritud graafikute kaupa. Pärast selle artikli lugemist saad ammendava idee funktsiooni väärtuste funktsioonist.
Alustame põhiliste määratlustega.
Määratlus 1.
Funktsioonide funktsiooni Y \u003d F (x) funktsioonide komplekt mõnel intervalli x on kõikide väärtuste kogum, mida see funktsioon võtab kõikide väärtuste vastastikmõju X ∈ X.
Määratlus 2.
Funktsiooni väärtuste funktsioon Y \u003d F (x) on kõigi selle väärtuste komplekt, mida ta võib võtta, kui X väärtused x ∈ f).
Mõne funktsiooni väärtuste vahemikus on tähistatud E (f) poolt.
Pange tähele, et paljude funktsiooniväärtuste kontseptsioon ei ole alati identne selle väärtuste pindalaga. Need mõisted on samaväärsed ainult siis, kui X väärtuste intervalliga, kui väärtuste kogum langeb kokku põllu määratlusega piirkonnaga.
Samuti on oluline eristada väärtuste vahemikku ja muutuja X lubatud väärtuste pindala ekspressiooniks õiges osas Y \u003d F (x). Lubatavate väärtuste X-väljendusrjade valik F (x) ja on selle funktsiooni määratlemise valdkond.
Järgnevalt näited, millele on näidatud mõned näited. Sinised jooned on funktsioonide graafikud, punased asümptotes, punased punktid ja jooned koordinaatteljedel on funktsioonide väärtuste valdkonnad.
Ilmselgelt saab funktsiooni funktsioonide funktsioonide funktsiooni O-teljel funktsiooni graafiku proaktiivses. Samal ajal võib see olla nii üks number kui ka paljud numbrid, segmendid, intervall, avatud tala, ühendades numbrilisi intervallidega jne.
Kaaluge peamisi viise funktsioonide funktsiooni funktsiooni leidmiseks.
Alustame teatud segmendi pideva funktsiooni väärtuste arvu määratlusega teatud segmendis [A; b]. Me teame, et funktsioon on pidev mõnel segmendil jõuab selle minimaalse ja maksimaalse, see tähendab, et suurim m x x ∈ a; b f (x) ja väikseim väärtus m i n x ∈ a; B F (x). See tähendab, et saame segmendi m i n x ∈ a; b f (x); m a x x ∈ a; B F (x), kus on algse funktsiooni palju väärtusi. Siis kõik, mida me peame tegema, on leida selle segmendi lõigatud minimaalsed punktid selle lõigu kohta.
Võtke ülesanne, milles peate määrama ARKSINUS väärtuste piirkonna.
Näide 1.
Tingimus: Leidke väärtuste väärtused Y \u003d R C Sin x.
Otsus
Üldisel juhul on ARXINUS määratluse valdkond segmendis [- 1; üks]. Me peame selle kindlaksmääratud funktsiooni suurima ja väikseima tähenduse kindlaksmäärama.
y "\u003d r c s sin x" \u003d 1 1 - x 2
Me teame, et tuletisinstrumentide funktsioon on positiivne kõigi X väärtuste jaoks, mis asuvad intervallis [- 1; 1], see tähendab kogu määratluse piirkonnas, suureneb Arksinus funktsioon. See tähendab, et see võtab väikseima väärtuse x, võrdne 1 ja suurim - x, võrdne 1.
m i n x ∈ - 1; 1 a r c patt x \u003d a r c patt - 1 \u003d - π 2 m x x ∈ - 1; 1 a r c patt x \u003d a r c patt 1 \u003d π 2
Seega on ARKSINUS funktsiooni väärtuste piirkonna võrdne E (R C pattu x) \u003d - π 2; π 2.
Vastus: E (r c s sin x) \u003d - π 2; π 2.
Näide 2.
Tingimus: Arvuta väärtused väärtused Y \u003d x 4-5 x 3 + 6 x 2 antud segmendis [1; neli].
Otsus
Kõik, mida me peame tegema, on arvutada suurim ja väikseim funktsiooni väärtus kindlaksmääratud intervalliga.
Eringempunktide määramiseks tuleb teha järgmised arvutused:
y "\u003d x 4 - 5 x 3 + 6 x 2" \u003d 4 x 3 + 15 x 2 + 12 x \u003d x 4 x 2 - 15 x + 12 y "\u003d 0 ⇔ x (4 x 2 - 15 x + 12 ) \u003d 0 x 1 \u003d 0 ∉ 1; 4 ja l ja 4 x 2 - 15 x + 12 \u003d 0 d \u003d - 15 2 - 4 · 4 · 12 \u003d 33 x 2 \u003d 15 - 33 8 ≈ 1. 16 ∈ 1 4; x 3 \u003d 15 + 33 8 ≈ 2. 59 ∈ 1; 4
Nüüd leiame kindlaksmääratud funktsiooni väärtused segmendi otstes ja punkte x 2 \u003d 15 - 33 8; x 3 \u003d 15 + 33 8:
y (1) \u003d 1 4 - 5 · 1 3 + 6 · 1 2 \u003d 2 a 15 - 33 8 \u003d 15 - 33 8 4 - 5 · 15 - 33 8 3 + 6 · 15 - 33 8 2 \u003d 117 + 165 33 512 ≈ 2. 08 Y 15 + 33 8 \u003d 15 + 33 8 4 - 5 · 15 + 33 8 3 + 6 · 15 + 33 8 2 \u003d 117-653 512 ≈ - 1. 62 y (4) \u003d 4 4 - 5 · 4 3 + 6 · 4 2 \u003d 32
See tähendab, et funktsioonide komplekt määratakse kindlaks segmendiga 117-16533 512; 32.
Vastus: 117 - 165 33 512 ; 32 .
Me pöördume leida mitmesuguseid väärtusi pideva funktsiooni Y \u003d F (x) väärtused intervallides (a; b) ja a; + ∞, - ∞; B, - ∞; + ∞.
Alustame selle suurema ja väikseima punkti määratlusega ning suurendavate ja kahanevate lüngad kindlaksmääratud intervalliga. Pärast seda peame arvutama ühepoolsed piirid intervalli otstes ja / või lõpmatuse piirangute otstes. Teisisõnu, me peame kindlaks määrama funktsiooni käitumise kindlaksmääratud tingimustes. Selleks on meil kõik vajalikud andmed.
Näide 3.
Tingimus: Arvutage funktsiooni Y \u003d 1 x 2 - 4 väärtused intervalliga (- 2; 2).
Otsus
Me määratleme funktsiooni suurim ja väikseim väärtus antud segmendis
y "\u003d 1 x 2 - 4" \u003d - 2 x (x 2 - 4) 2 Y "\u003d 0 ⇔ - 2 x (x 2 - 4) 2 \u003d 0 ⇔ x \u003d 0 ∈ (- 2; 2)
Meil oli maksimaalne väärtus 0, sest see oli praegu, et funktsioon funktsioon funktsioon ja ajakava liigub kahanevasse. Vt Illustration:
See tähendab, Y (0) \u003d 1 0 2 - 4 \u003d - 1 4 on maksimaalne funktsiooni väärtused.
Nüüd me määratleme käitumise funktsiooni sellise x, mis püüab - 2 paremal küljel ja K + 2 vasakul küljel. Teisisõnu leiame ühepoolsed piirid:
lim X → - 2 + 0 1 x 2 - 4 \u003d Lim x → 2 + 0 1 (x-2) (x + 2) \u003d 1-2 + 0 - 2-2 + 0 + 2 \u003d - 1 4 · 1 + 0 \u003d - ∞ Lim X → 2 + 0 1 x 2 - 4 \u003d Lim x → 2 + 0 1 (x-2) (x + 2) \u003d 1 2-0-22 - 0 + 2 \u003d 1 4 · 1 - 0 \u003d - ∞
Vajame, et funktsiooni väärtused suurenevad miinus lõpmatusest - 1 4-ni, kui argument varieerub vahemikus - 2 kuni 0. Ja kui argument varieerub 0 kuni 2, vähenevad funktsiooni väärtused miinus lõpmatuseni. Järelikult on määratud funktsiooni väärtuste kogum soovitud intervalliga (- ∞; - 1 4].
Vastus: (- ∞ ; - 1 4 ] .
Näide 4.
Seisukord: Täpsustage Y \u003d t G x komplekt antud intervalliga - π 2; π 2.
Otsus
Me teame, et üldisel juhul derivaat puutuja B - π 2; π 2 on positiivne, st funktsioon suureneb. Nüüd me defineerime, kuidas funktsioon on käitunud määratud piires:
lim x → π 2 + 0 t g x \u003d t g - π 2 + 0 \u003d - ∞ lim x → π 2 - 0 t g x \u003d t g π 2 - 0 \u003d + ∞
Me saime suurendada väärtused funktsiooni miinus lõpmatuse pluss lõpmatuse, kui argument on muutunud - π 2 kuni π 2, ja võib öelda, et palju kehtivaid numbreid on palju lahendusi See funktsioon.
Vastus: - ∞ ; + ∞ .
Näide 5.
Tingimus: Määrake kindlaks, milline on loodusliku logaritmi funktsiooni väärtuste pindala \u003d ln x.
Otsus
Me teame, et see funktsioon on määratletud argumendi D (Y) \u003d 0 positiivsete väärtustega \u003d 0; + ∞. Määratud intervalli derivaat on positiivne: y "\u003d ln x" \u003d 1 x. Niisiis on funktsiooni suurenemine. Järgmisena peame määrama ühepoolse piiri juhul, kui argument kipub 0 (paremas osas) ja kui X kipub lõpmatuseni:
lim x → 0 + 0 ln x \u003d ln (0 + 0) \u003d - ∞ Lim x → ∞ ln x \u003d ln + ∞ \u003d + ∞
Me saavutasime, et funktsiooni funktsioone suureneb miinus lõpmatusest pluss lõpmatuse muutes X väärtused nullist pluss lõpmatuseni. See tähendab, et kõikide kehtivate numbrite kogum on loodusliku logaritmi funktsiooni väärtuste valdkond.
Vastus:kõikide kehtivate numbrite komplekt on loodusliku logaritmi funktsiooni väärtuste valdkond.
Näide 6.
Tingimus: Määrake kindlaks, milline on funktsiooni Y \u003d 9 x 2 + 1 väärtuste hulk.
Otsus
See funktsioon määratakse seisundi all, et X on kehtiv number. Arvutame funktsioonide suurimaid ja väiksemaid väärtusi, samuti selle suurenemise ja kahanemise lüngad:
y "\u003d 9 x 2 + 1" \u003d - 18 x (x 2 + 1) 2 y "\u003d 0 ⇔ x \u003d 0 y" ≤ 0 ⇔ x ≥ 0 y "≥ 0 ⇔ x ≤ 0 0
Selle tulemusena otsustasime, et see funktsioon väheneb, kui x ≥ 0; suurendada, kui x ≤ 0; Sellel on maksimaalne punkt y (0) \u003d 9 0 2 + 1 \u003d 9 muutujaga, mis on võrdne 0-ga.
Vaatame, kuidas funktsioon käitub lõpmatusse:
lim X → - ∞ 9 x 2 + 1 \u003d 9 - ∞ 2 + 1 \u003d 9 · 1 + ∞ \u003d + 0 Lim x → + ∞ 9 x 2 + 1 \u003d 9 + ∞ 2 + 1 \u003d 9 · 1 + ∞ \u003d + 0.
Seda saab näha registrist, et funktsiooni väärtused käesoleval juhul läheneb asümptotiliselt 0-le.
Olgem kokku: Kui argument varieerub miinus lõpmatusest nullini, suurenevad funktsiooni väärtused 0 kuni 9. Kui argumendi väärtused varieeruvad 0-lt pluss lõpmatusest, väheneb funktsiooni vastavad väärtused 9 kuni 0-ni. Me näitasime seda pildil:
See näitab, et funktsiooni väärtuste pindala on intervalli E (Y) \u003d (0; 9]
Vastus: E (y) \u003d (0; 9]
Kui me peame määrama funktsiooni funktsiooni Y \u003d F (x) funktsioonide komplekti [A; b), (a; b], [a; + ∞), (- ∞; b], peame täitma täpselt sama uuringuid. Me ei lahti neid juhtumeid: siis nad jätkavad meid ülesannetes .
Aga kuidas olla, kui mõne funktsiooni määratluse valdkond on mitme intervalli kombinatsioon? Siis peame arvutama paljude nende lünkade paljude väärtuste arvutamiseks ja nende ühendamiseks.
Näide 7.
Tingimus: Määrake, milline on väärtuste ala y \u003d x x - 2.
Otsus
Kuna funktsiooni nimetaja ei tohiks seisata 0, siis d (y) \u003d - ∞; 2 ∪ 2; + ∞.
Alustame esimese segmendi funktsiooni väärtuste määratluse määratlusega - ∞; 2, mis on avatud tala. Me teame, et selle funktsioon on vähenenud, st selle funktsiooni tuletisinstrument on negatiivne.
lim x → 2 - 0 xx - 2 \u003d 2 - 0 2 - 0 - 2 \u003d 2 - 0 \u003d - ∞ Lim x → - ∞ xx - 2 \u003d lim x → - ∞ x - 2 + 2 x - 2 \u003d lim x → - ∞ 1 + 2 x - 2 \u003d 1 + 2 - ∞ - 2 \u003d 1 - 0
Siis juhtudel, kui argument varieerub miinus lõpmatuse poole, läheneb funktsiooni väärtused asümptootiliselt 1. Kui X väärtused varieeruvad miinus lõpmatusest 2, vähenevad väärtused 1 kuni miinus lõpmatuseni, st Selle segmendi funktsioon võtab väärtusi intervallist - ∞; üks. Me välistame üksus meie põhjendusest, kuna funktsiooni väärtused ei jõua selle juurde, vaid ainult asümptootiliselt läheneb sellele.
Avatud tala jaoks 2; + ∞ Toodame täpselt samu tegevusi. Selle funktsioon on ka kahanev:
lim x → 2 + 0 xx - 2 \u003d 2 + 0 2 + 0 - 2 \u003d 2 + 0 \u003d + ∞ lim x → + ∞ xx - 2 \u003d lim x → + ∞ x - 2 + 2 x - 2 \u003d lim x → + ∞ 1 + 2 x - 2 \u003d 1 + 2 + ∞ - 2 \u003d 1 + 0
Selle segmendi funktsiooni väärtused määravad komplekti 1 abil; + ∞. See tähendab, et seisundis määratud funktsiooni väärtuste piirkonda seostatakse SET-∞-ga; 1 ja 1; + ∞.
Vastus: E (y) \u003d - ∞; 1 ∪ 1; + ∞.
Seda saab näha ajakava:
Erijuhtum on perioodilised funktsioonid. Nende väärtuse ala langeb kokku selle lõhe paljude väärtustega, mis vastab selle funktsiooni perioodile.
Näide 8.
Tingimus:määrake sinuse väärtuste ala Y \u003d sin x.
Otsus
Sinus viitab perioodilisele funktsioonile ja selle periood on 2 Pi. Me võtame segmendi 0; 2 π ja vaata, mida paljud väärtused on.
y "\u003d (sin x)" \u003d cos x y "\u003d 0 ⇔ cos x \u003d 0 ⇔ x \u003d π 2 + πk, k ∈ z
0; 2 π Funktsioon on äärmuslikud punktid π 2 ja x \u003d 3 π 2. Arvutame, millised funktsiooni väärtused nendes on võrdsed, samuti segmendi piiridel, pärast mida me valime suurima ja väikseima väärtuse.
y (0) \u003d sin 0 \u003d 0 y π 2 \u003d pat π 2 \u003d 1 y 3 π 2 \u003d sin 3 π 2 \u003d - 1 y (2 π) \u003d patt (2 π) \u003d 0 ⇔ min x ∈ 0; 2 π sin x \u003d sin 3 π 2 \u003d - 1, max x ∈ 0; 2 π Sin x \u003d sin π 2 \u003d 1
Vastus: E (pattu x) \u003d - 1; üks.
Kui teil on vaja teada funktsioonide väärtuste, näiteks võimsuse, soovitusliku, logaritmiku, trigonomeetrilise, inverse trigonomeetrilise, siis soovitame lugeda uuesti artikli põhifunktsioonide artikkel. Teooria, mida me siin anname, võimaldab teil kontrollida seal näidatud väärtusi. On soovitav õppida, sest probleemide lahendamisel on sageli vajalikud. Kui teate põhifunktsioonide väärtuste vahemikku, saate hõlpsasti leida elementaarsest saadud funktsioone, kasutades geomeetrilist konversiooni.
Näide 9.
Tingimus: Määrata väärtus väärtuse Y \u003d 3 A RC COS x 3 + 5 π 7 - 4.
Otsus
Me teame, et segment 0 kuni PI-l on arkkosiini väärtuste pindala. Teisisõnu, E (R C COS X) \u003d 0; π või 0 ≤ a r c cos x ≤ π. Saame funktsiooni A RC COS X 3 + 5 π 7 Arcsiinusest, nihutades ja venitades seda mööda O x telge, kuid sellised muutused ei anna meile midagi. Niisiis, 0 ≤ r c cos x 3 + 5 π 7 ≤ π.
Funktsioon 3 A R C COS x 3 + 5 π 7 võib saada arosiinist A R C COS X 3 + 5 π 7, venitades piki ordinaat telge, st. 0 ≤ 3 a r c cos x 3 + 5 π 7 ≤ 3 π. Lõplik konversioon muutub 4 väärtusele O-teljel. Selle tulemusena saame topelt ebavõrdsuse:
0 - 4 ≤ 3 a r c cos x 3 + 5 π 7 - 4 ≤ 3 π - 4 ⇔ - 4 ≤ 3 arccos x 3 + 5 π 7 - 4 ≤ 3 π - 4
Me saime, et väärtuste väärtus on vaja on võrdne e (y) \u003d - 4; 3 π - 4.
Vastus: E (y) \u003d - 4; 3 π - 4.
Teine näide Kirjutage ilma selgituseta alla, sest See on täiesti sarnane eelmisele.
Näide 10.
Tingimus: Arvutage, milline on funktsiooni Y \u003d 2 2 x - 1 + 3 väärtuste pindala.
Otsus
Me kirjutame välja tingimuses nimetatud funktsiooni Y \u003d 2 · (2 \u200b\u200bx-1) - 1 2 + 3. Toitefunktsiooni Y \u003d X - 1 2 puhul määratakse väärtuste piirkond intervallile 0; + ∞, s.o. X - 1 2\u003e 0. Sel juhul:
2 x - 1 - 1 2\u003e 0 ⇒ 2 · (2 \u200b\u200bx - 1) - 1 2\u003e 0 ⇒ 2 · (2 \u200b\u200bx-1) - 1 2 + 3\u003e 3
See tähendab E (y) \u003d 3; + ∞.
Vastus: E (y) \u003d 3; + ∞.
Nüüd analüüsime, kuidas leida funktsiooni funktsiooni, mis ei ole pidev. Selleks peame jagama kogu ala intervallidesse ja leidma paljude nende jaoks palju väärtusi, seejärel ühendage see, mis juhtus. Et seda paremini mõista, soovitame teil korrata katkematute punktide põhivaateid.
Näide 11.
Tingimus: Funktsioon y \u003d 2 pattu x 2 - 4, x ≤ - 3 - 1, - 3< x ≤ 3 1 x - 3 , x > 3. Arvuta oma väärtuste pindala.
Otsus
See funktsioon on määratletud kõigi X väärtuste jaoks. Me teostame oma analüüsi argumendi väärtuste järjepidevuse eest - 3 ja 3:
lim x → - 3 - 0 f (x) \u003d lim x → - 3 2 pattu x 2 - 4 \u003d 2 sin - 3 2 - 4 \u003d - 2 sin 3 2 - 4 lim x → - 3 + 0 f (x) \u003d Lim x → - 3 (1) \u003d - 1 ⇒ lim x → - 3 - 0 f (x) ≠ lim x → - 3 + 0 f (x)
Meil on mitteresistentne lõhe esimesest liiki, kui argument on hinnatud - 3. Selle lähenemisel püüavad funktsiooni väärtused - 2 pattu 3 2 - 4 ja kui X K-3 püüab paremal pool, püüab väärtused - 1.
lim X → 3 - 0 F (x) \u003d Lim X → 3 - 0 (- 1) \u003d 1 Lim x → 3 + 0 f (x) \u003d lim x → 3 + 0 1 x - 3 \u003d + ∞
Meil on punktis 3 mitte-vastupidav lõhe. Kui funktsioon püüab selle vastu, lähenevad selle väärtused - 1, kui püüate samal hetkel paremale - miinus lõpmatusse.
See tähendab, et kogu selle funktsiooni määramise valdkond on jaotatud 3 intervallidega (- ∞; - 3], (- 3; 3], (3; + ∞).
Esimesel neist tegime välja funktsioon y \u003d 2 pattu x 2 - 4. Alates - 1 ≤ Sin x ≤ 1, saame:
1 ≤ Sin x 2< 1 ⇒ - 2 ≤ 2 sin x 2 ≤ 2 ⇒ - 6 ≤ 2 sin x 2 - 4 ≤ - 2
Niisiis, antud intervalliga (- ∞; - 3], on funktsiooni seadistatud väärtus [- 6; 2].
Semi-intervalli (- 3; 3] konstantse funktsioon Y \u003d - 1 saadi. Seetõttu vähendatakse kõiki paljusid selle väärtusi antud juhul ühele numbrile - 1.
Teise intervalliga 3; + ∞ Meil \u200b\u200bon funktsioon y \u003d 1 x - 3. See on kahanevalt, sest y "\u003d - 1 (x - 3) 2< 0 . Она будет убывать от плюс бесконечности до 0 , но самого 0 не достигнет, потому что:
lim X → 3 + 0 1 X - 3 \u003d 1 3 + 0 - 3 \u003d 1 + 0 \u003d + ∞ Lim x → + ∞ 1 x - 3 \u003d 1 + ∞ - 3 \u003d 1 + ∞ + 0
See tähendab, et esmaste funktsioonide väärtuste kogum x\u003e 3 on komplekt 0; + ∞. Nüüd ühendame saadud tulemused: E (Y) \u003d - 6; - 2 ∪ - 1 ∪ 0; + ∞.
Vastus: E (y) \u003d - 6; - 2 ∪ - 1 ∪ 0; + ∞.
Lahendus kuvatakse ajakava järgi:
Näide 12.
Seisund: On funktsioon Y \u003d x 2 - 3 E x. Määrata oma väärtuste kogum.
Otsus
See on määratletud kõigi väidete väärtuste jaoks, mis kehtivad kehtivad numbrid. Me määratleme, millistes intervallides see funktsioon suureneb ja millises vähenes:
y "\u003d x 2 - 3 E x" \u003d 2 x E x - E x (x 2 - 3) E 2 x \u003d - x 2 + 2 x + 3 E x \u003d - (x + 1) (x - 3) e x
Me teame, et tuletisütlev tuletis pöördub 0, kui x \u003d - 1 ja x \u003d 3. Asetame need kaks punkti teljele ja selgitage välja, millised märgid on saadud ajavahemike järel derivaat.
Funktsioon väheneb (- ∞; - 1] ∪ [3; + ∞) ja suurendada [- 1; 3]. Minimaalse punkti punkt on 1, maksimaalne - 3.
Nüüd leiame funktsiooni sobivad väärtused:
y (- 1) \u003d - 1 2 - 3 E - 1 \u003d - 2 E y (3) \u003d 3 2-3 E 3 \u003d 6 E - 3
Vaatame selle funktsiooni käitumist Infinity:
lim x → - ∞ x 2 - 3 ex \u003d - ∞ 2 - 3 e - ∞ \u003d + ∞ + 0 \u003d + ∞ Lim x → + ∞ x 2 - 3 ex \u003d + ∞ 2 - 3 E + ∞ \u003d + ∞ + ∞ \u003d \u003d lim x → + ∞ x 2 - 3 "ex" \u003d lim x → + ∞ 2 XEX \u003d + ∞ + ∞ \u003d \u003d \u003d lim x → + ∞ 2 x "(ex)" \u003d 2 lim x → + ∞ 1 Ex \u003d 2 · 1 + ∞ \u003d + 0
Teise piirmäära arvutamiseks kasutati Lopital reeglit. Pange meie otsuse kursus ajakavale.
See näitab, et funktsiooni väärtused vähenevad lõpmatuse pluss-2 E-st, kui argument varieerub miinus lõpmatusest - 1. Kui see muutub 3-st pluss lõpmatusest, vähenevad väärtused 6 E-3 kuni 0-ni, kuid seda ei saavutata.
Seega e (y) \u003d [- 2 e; + ∞).
Vastus: E (y) \u003d [- 2 e; + ∞)
Kui märkate teksti viga, valige see ja vajutage Ctrl + Enter
Page 1
Õppetund 3.
"Funktsiooniväärtused"
Eesmärgid: - Rakenda konkreetse ülesande lahendamiseks väärtuste vahemiku mõiste;
tüüpiliste ülesannete lahendamine.
Juba mitu aastat ilmuvad eksamid regulaarselt ülesandeid, milles sellest funktsioonide perekonnast nõuab, et rõhutada neid, kelle väärtuste kogumid vastavad deklareeritud tingimustele.
Mõtle seda ülesannet.
Teadmiste tegelikkus.
Mida me mõistame funktsiooni väärtuste hulgast?
Kuidas tähendada funktsiooniväärtuste komplekt?
Milliseid andmeid leiame palju funktsioone väärtusi? (Vastavalt funktsiooni analüütilisele registrile või selle ajakavale)
(Vt EGE, A osa ülesanne)
Paljud väärtused milliseid funktsioone me teame? (Loetletud peamised ülesanded nende sisenemisega juhatusele; iga funktsiooni jaoks on kirjutatud paljudele väärtustele). Selle tulemusena pardal ja sülearvuti õpilastel
|
Ülesanne |
Paljud väärtused |
|
y. = x. 2 y. = x. 3 y \u003d.| x.| y \u003d.
|
E ( y.) = E ( y.) = [- 1, 1] E ( y.) = (– ∞, + ∞) E ( y.) = (– ∞, + ∞) E ( y.) = (– ∞, + ∞) E ( y.) = (0, + ∞) |
Kas me saame kasutada seda teadmisi, leida kohe mitmeid väärtusi, mis on registreeritud juhatuse ülesannete? (Vt tabel 2).
Mis aitab sellele küsimusele vastuseks? (Nende funktsioonide graafikud).
Kuidas ehitada esimese funktsiooni graafik? (Alandage parabool 4 ühiku alla).
|
Ülesanne |
Paljud väärtused |
|
y. = x. 2 – 4 |
E ( y.) = [-4, + ∞) |
|
y. = + 5 |
E ( y.) = |
|
y. = - 5 cos. x. |
E ( y.) = [- 5, 5] |
|
y \u003d.tG ( x +. / 6) – 1 |
E ( y.) = (– ∞, + ∞) |
|
y \u003d.patt ( x +. / 3) – 2 |
E ( y.) = [- 3, - 1] |
|
y \u003d.| x. – 1 | + 3 |
E ( y.) = |
|
y \u003d.| CTG. x.| |
E ( y.) = |
|
y. =  \u003d | Cos (x + / 4) | |
E ( y.) = |
|
y \u003d.(x -5) 2 + 3 |
E ( y.) = . Leia erinevaid funktsioone:   . 
Sissejuhatus Algoritm probleeme lahendamisel trigonomeetriliste funktsioonide väärtuste leidmiseks. Vaatame, kuidas me saame rakendada olemasolevat kogemust erinevate ülesannete lahendamiseks ühe eksami võimalusi. 1. argumendiga seotud funktsioonide leidmine. Näide. Leia funktsiooni väärtus Y \u003d 2 cos.(π / 2 + π / 4 ) – 1, kui a x \u003d - π / 2. Otsus. y.(-π / 2) \u003d 2 cos.(- π / 2 - π / 4 )- 1= 2 cos.(π / 2 + π / 4 )- 1 = - 2 patt. π / 4 - 1 \u003d - 2  – 1 =
= – 2. trigonomeetriliste funktsioonide väärtuste pindala
1≤ patt. H.≤ 1 2 ≤ 2 patt. H.≤ 2 9 ≤ 11+2patt. H.≤ 13 3 ≤ Me tõrjume funktsiooni täisarvu väärtused intervallile. See on number 3. Vastus: 3.
w.= patt. 2 x-2 · 3. patt. X +.3 2 - 3 2 + 8, w.= (patt. x-3) 2 -1. E ( patt. H.) = [-1;1]; E ( patt. H. -3) = [-4;-2]; E ( patt. H. -3) 2 = ; E ( w.) = . Vastus :.
Kas me leiame selle funktsiooni palju väärtusi? (Mitte.) Mida tuleks teha? (Vähendage ühe funktsiooni.) Kuidas seda teha? (Kasutage COS 2 valemit x. \u003d 1-sin 2 x..) Niisiis, w. \u003d 1-sin 2 x. + 2Sin x. –2, y. \u003d -Sin 2. x. + 2Sin x. –1, w. \u003d - (patt x. –1) 2 . Noh, nüüd leiame palju väärtusi ja valida väikseima neist. 1 ≤ patt. x. ≤ 1, 2 ≤ patt. x. – 1 ≤ 0, 0 ≤ (patt x. – 1) 2 ≤ 4, 4 ≤ - (patt x. -1) 2 ≤ 0. See tähendab funktsiooni väikseimat väärtust w. naim \u003d -4. Vastus: -4.
Otsus. w. \u003d 1-cos 2 x. + Cos. x. + 1,5, w. \u003d -COS 2. x. + 2 ∙ 0,5 ∙ cos x. - 0,25 + 2,75, w. \u003d - (cos x.- 0,5) 2 + 2,75. E (cos. x.) = [-1;1], E (cos. x. – 0,5) = [-1,5;0,5], E (cos. x. – 0,5) 2 = , E (- cos x.-0,5) 2) = [-2,25;0], E ( w.) = . Funktsiooni suurim väärtus w. naer \u003d 2,75; Väikseim väärtus w. naim \u003d 0,5. Leia toote suurima ja väikseima funktsiooni toode: w. naer ∙ W. naim = 0,5∙2,75 = 1,375. Vastus: 1.375. Otsus. Kirjutage funktsioon vormis ümber w. =, w. = Nüüd leiame palju funktsioone väärtusi. E (patt x.) = [-1, 1], E (6sin. x.) = [-6, 6], E (6sin. x. + 1) = [-5, 7], E ((6sin) x. + 1) 2) = , E (- (6sinin) x. + 1) 2) = [-49, 0], E (- (6sinin) x. + 1) 2 + 64) = , E ( y.) = [ Me leiame summa kogu väärtuste funktsiooni: 4 + 5 + 6 + 7 + 8 \u003d 30. Vastus: 30.  Otsus. 1) 2) Seetõttu 2. h. II kvartali kuuluv. 3) teises kvartalis väheneb sinuse funktsioon ja see on pidev. Nii et see funktsioon 4) Arvutage need väärtused:
Vastus :
 Otsus. 1) Kuna sinus võtab väärtusi -1-1-1, siis erinevuste väärtuste kogum 2) Arkkosiinus - monotoonselt väheneb ja pidev funktsioon. Nii palju ekspressiooniväärtusi on segment 3) selle segmendi korrutamisel Vastus:  Otsus. Kuna arctanens on kasvav funktsioon, 2) suurendamisel h. alates 3) suurendades 4) Kasutades valemiga, väljendades sinust läbi poole nurga tangendi, leiame selle
Niisiis, soovitud väärtuste kogum on segmentide kombinatsioon Vastus: w. \u003d pattu x + b cos xvõi w. \u003d patt (ribax) + b cos (riba x).
Otsus. Väärtuse leidma Me muudame väljendit 15 Sin 2x + 20 cos 2x \u003d 25 ( 25 patt (2x + Paljud funktsioonide väärtused Y \u003d patt (2x + Siis palju esialgseid funktsiooni väärtusi -25 Vastus:
[-25; 25].
Ülesanne w. \u003d CTG. h. langeb segmendile [π / 4; π / 2] Seetõttu võtab väikseim väärtus funktsiooni, millal x \u003d π / 2, see on w.(π / 2) \u003d CTG π / 2 \u003d 0; Ja suurim väärtus - millal x \u003d π / 4, see on w.(π / 4) \u003d CTG π / 4 \u003d 1. Vastus: 1, 0.  . Otsus. Me rõhutame võrdõiguslikkust Sellest järeldub, et funktsioon f (x) on kas hüperbool (a ≠ 0) või sirge punkti. Samal ajal, kui a; 2a) ja (2a; Kui a \u003d 0, siis f (x) \u003d -2 kogu määratluse ala x ≠ 0. Seetõttu on ilmselge, et soovitud parameetri väärtused ei ole võrdsed nulliga. Kuna me oleme huvitatud funktsiooni väärtustest ainult segmendis [-1; 1], olukordade klassifikatsioon määratakse kindlaks asjaoluga, et asümptota x \u003d 2a hüperboolid (a ≠ 0) asub selle segmendi suhtes võrreldes. Juhtum 1. Kõik intervalli punktid [-1; 1] asuvad vertikaalsete asümptoteide X \u003d 2a paremal, st kui 2a Juhtum 2. Vertikaalne Asümptota ületab intervalli [-1; 1] ja funktsioon väheneb (nagu 1), st millal Juhtum 3. Vertikaalne asümptota ületab intervalli [-1; 1] Ja funktsioon suureneb, st, -1 Juhtum 4. Iga intervalli punktid [-1; 1] asuvad vertikaalsete asümptoteide vasakul pool, st 1 a\u003e. ja teine Vastuvõtt 5. Fraktsioonilise ratsionaalse funktsiooni määratlemise valemi lihtsustamine Vastuvõtt 6. Paljude ruutfunktsioonide leidmine (parabooli tippu leidmine ja selle harude käitumise iseloomustus). Vastuvõtt 7. Lisanurga sissetoomine mõnede trigonomeetriliste funktsioonide väärtuste leidmiseks. Funktsioon on üks tähtsamaid matemaatilisi kontseptsioone. Määratlus: Kui iga number teatud komplekti x pannakse vastavalt ühe numbri y, nad ütlevad, et funktsioon Y (X) on määratud selles komplektis. Samal ajal nimetatakse x sõltumatu muutujaks või argumentiks ja y-sõltuva muutujaks või funktsiooni või lihtsuse väärtusest. Samuti on öeldud, et muutuja Y on funktsioon muutuja X funktsioon. Kirjeldades teatava kirja kirjavahetust, näiteks F, on mugav kirjutada: Y \u003d F (x), st Y-i väärtus saadakse X-st argumendist sobitamisega f. (Loe: Y võrdselt f alates x.) Sümbol f (x) tähistavad funktsiooni väärtust, mis vastab x-ga võrdse argumendi väärtusele. Näide 1 Olgu funktsioon määrab valemiga Y \u003d 2x 2 -6. Siis saab kirjutada, et f (x) \u003d 2x 2 -6. Leidke x väärtuste funktsiooni väärtused, mis on võrdsed näiteks 1; 2,5; -3; s.o leiame F (1), F (2,5), F (-3): f (1) \u003d 2 1 2 -6 \u003d -4; Pange tähele, et vormi Y \u003d F (x) salvestamisel kasutatakse F-i asemel muud tähti: g, ja nii edasi. Määratlus: funktsiooni määratluspiirkond - need on kõik X väärtused, mille juures on funktsioon. Kui funktsiooni määratletakse valemiga ja selle määratluse ala ei ole täpsustatud, arvatakse, et funktsiooni määramise funktsioon koosneb kõigist argumendi väärtustest, milles valem on mõtet. Teisisõnu, valemiga määratud funktsiooni määratluse piirkond on kõik argumendi väärtused, välja arvatud need, mis toovad kaasa meetmetele, mida me ei saa täita. Praegu me teame ainult kaks sellist tegevust. Me ei saa jagada null ja ei saa eemaldada ruutjuur negatiivse numbri. Määratlus: kõik väärtused, mida ülalpeetav muutuja moodustab funktsiooniväärtuse ala. Tegelikku protsessi kirjeldavat määratlust sõltub selle voolu eritingimustest. Näiteks sõltuvus pikkus L rauast varras kuumutamisel T-d ekspresseeritakse valemiga, kus L 0 varda esialgne pikkus ja lineaarne laienemisrakk. Määratud valem on mõtet T. mis tahes väärtustel. Funktsiooni määratluse pindala \u003d g (t) on siiski mitme kümne kraadi vahe, mille jaoks lineaarse laienemise seadus on õiglane. Näide. Määrake funktsiooni väärtuste funktsioon. y \u003d arcsiinx. Otsus. ARKSINUS Määratluspiirkond on segment [-1; 1]
. Leia selle segmendi funktsiooni suurim ja väikseim väärtus. Derivaat on kõigi jaoks positiivne x. Intervallilt (-1; 1)
See tähendab, et ARKSINUS funktsioon suureneb kogu määratluse piirkonnas. Seetõttu võtab see väikseim väärtus x \u003d -1.ja suurim x \u003d 1.. Meil on Arksinus funktsioonide väärtuste hulk Leia palju funktsiooni väärtusi Otsus. Me leiame selle segmendi funktsiooni suurima ja väikseima väärtuse. Määrake segmendile kuuluvate äärmuspunktide
:  Värsked artiklid
|
– 1.
. E (y) \u003d.
,
, 8].
i.e h. Kuulub I kvartali.
enne 
.
. Korrutades 
See segment läheb segmendiks 
.
.
Vastu võtma 
.
.
.
enne 
Argument 2. h. suureneb 
enne 
. Kuna sinus suureneb sellise lõhega, siis funktsioon 
Kuni 1.
Argument 2. h. suureneb 
. Kuna sinus väheneb sellise lõhega, siis funktsioon 
Kuni 1.
.
ja 
See tähendab segment 
= 
= 25.
) = 25 () =
) Kus cos 
Patt (2x + 
) Ja kui A\u003e 0, suureneb nendel kiirtetel monotoonselt.
.
.
Lõigatud
.
